
题目列表(包括答案和解析)
19.证明: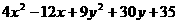
=4 x2-12x+9+9 y2+30y+25+1
=(2x-3) 2+(3y+5) 2+1
≥1.
17.证明: 原式=31998(32-4×3+10)= 31998×7,
∴ 能被7整除。
15.解:原式=(x+2)(3x+5)
提示:把二次项3x2分解成x与3x(二次项一般都只分解成正因数),常数项10可分成1×10=-1×(-10)=2×5=-2×(-5),其中只有11x=x×5+3x×2。
说明:十字相乘法是二次三项式分解因式的一种常用方法,特别是当二次项的系数不是1的时候,给我们的分解带来麻烦,这里主要就是讲讲这类情况。分解时,把二次项、常数项分别分解成两个数的积,并使它们交叉相乘的积的各等于一次项。需要注意的是:⑴如果常数项是正数,则应把它分解成两个同号的因数,若一次项是正,则同正号;若一次项是负,则应同负号。⑵如果常数项是负数,则应把它分解成两个异号的因数,交叉相乘所得的积中,绝对值大的与一次项的符号相同(若一次项是正,则交叉相乘所得的积中,绝对值大的就是正号;若一次项是负,则交叉相乘所得的积中,绝对值大的就是负号)。
ax c
 二次项 常数项
二次项 常数项
bx d
 adx+bcx=(ad+bc)x 一次项
adx+bcx=(ad+bc)x 一次项
ab x2+(ad+bc)x+cd=(ax+c)(bx+d)
14. 解 原式=(x+2)(x+1)(x+4)(x+3)-120
=(x+2)(x+3)(x+1)(x+4)-120
=( x2+5x+6)( x2+5x+4)-120
令 x2+5x=m, 代入上式,得
原式=(m+6)(m+4)-120=m2+10m-96
=(m+16)(m-6)=( x2+5x+16)( x2+5x-6)=( x2+5x+16)(x+6)(x-1)
提示:把x2+5x看成一个整体。
13.解:原式=[(x+1)(x+4)][(x+2)(x+3)]+1
=( x2+5x+4)( x2+5x+6)+1
令x2+5x=a,则 原式=(a+4)(a+6)+1
=a2+10a+25
=(a+5)2
=(x2+5x+5)
提示:把x2+5x看成一个整体。
12.解:原式=3(x2+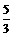 x)-2
x)-2
=3(x2+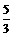 x+
x+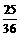 -
-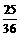 )-2 *
)-2 *
=3(x+ )2-3×
)2-3×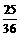 -2
-2
=3(x+ )2-
)2-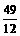
=3[(x+ )2-
)2-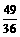 ]
]
=3(x+ +
+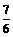 )(x+
)(x+ -
-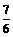 )
)
=3(x+2)(x-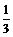 )
)
=(x+2)(3x-1)
提示:*这步很重要,根据完全平方式的结构配出来的。对于任意二次三项式ax2+bx+c(a≠0)可配成a(x+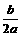 )2+
)2+ .
.
11.解:原式=x2-2x+1-1-8 *
=(x-1)2-32
=(x-1+3)(x-1-3)
=(x+2)(x-4)
提示:本题用了配方法,将x2-2x加上1个“1”又减了一个“1”,从而构成完全平方式。
10.解:原式=(a2+b2 +2ab)+2bc+2ac+c2
=(a+b)2+2(a+b)c+c2
=(a+b+c)2
提示:*将(a+b)视为 1个整体。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com