
题目列表(包括答案和解析)
2、?比较下列每对数的大小:
(1)-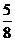 与-
与-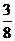 ;(2)-
;(2)-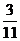 与-0?273;(3)-
与-0?273;(3)-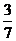 与-
与-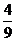 ;
;
(4)- 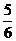 与-
与-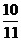 ;(5)-
;(5)- 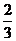 与-
与-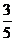 ;(6)-
;(6)- 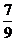 与-
与-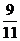
1、?判断下列各式是否正确:
(1)|-0?1|<|-0?01|; (2)|- 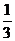 |<
|<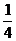 ; (3)
; (3) 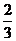 <
<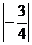 ; (4)
; (4)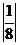 >-
>-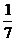 ?
?
(四)、小结
先由学生叙述比较有理数大小的两种方法--利用数轴比较大小;利用绝对值比较大小,然后教师引导学生得出:比较两个有理数的大小,实际上是由符号与绝对值两方面来确定?学习了绝对值以后,就可以不必利用数轴来比较两个有理数的大小了?
(三)、运用举例 变式练习
例1 比较-4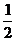 与-|-3|的大小?
与-|-3|的大小?
例2 已知a>b>0,比较a,-a,b,-b的大小?
例3 比较-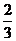 与-
与-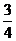 的大小?
的大小?
课堂练习
1、?比较下列每对数的大小:
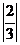 与
与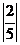 ;|2|与
;|2|与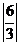 ;-
;-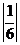 与
与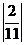 ;
; 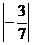 与
与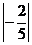 ?
?
2、?比较下列每对数的大小:
-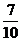 与-
与-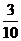 ;-
;-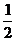 与-
与-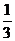 ;-
;-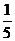 与-
与-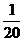 ;-
;-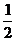 与-
与-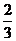 ?
?
(二)、师生共同探索利用绝对值比较负数大小的法则
利用数轴我们已经会比较有理数的大小?
由上面数轴,我们可以知道c<b<a,其中b,c都是负数,它们的绝对值哪个大?显然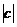 >
>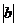 引导学生得出结论:
引导学生得出结论:
两个负数,绝对值大的反而小?这样以后在比较负数大小时就不必每次再画数轴了?
(一)、从学生原有认知结构提出问题
1、计算:|+1?5|;|-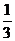 |;|0|?
|;|0|?
2、计算:|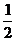 -
-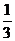 |;|-
|;|-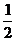 -
-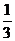 |.
|.
3、比较-(-5)和-|-5|,+(-5)和+|-5|的大小?
4、哪个数的绝对值等于0?等于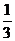 ?等于-1?
?等于-1?
5、绝对值小于3的数有哪些?绝对值小于3的整数有哪几个?
6、a,b所表示的数如图所示,求|a|,|b|,|a+b|,|b-a|?
7、若|a|+|b-1|=0,求a,b?
这一组题从不同角度提出问题,以使学生进一步掌握绝对值概念?
解:1、?|+1?5|=1?5,|-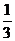 |=
|=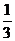 ,|0|=0?
,|0|=0?
让学生口答这样做的依据?
2、?|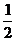 -
-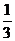 |=|
|=|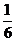 |=
|=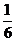 |,|-
|,|-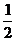 -
-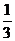 =-(-
=-(-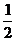 -
-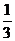 )。?
)。?
说明:“| |”有两重作用,即绝对值和括号?
3、?因为-(-5)=5,-|-5|=-5,5>-5,
所以-(-5)>-|-5|。?
这里需讲清一个问题,即-(-5)和-|-5|的读法,让学生熟悉,-(-5)读作-5的相反数,-|-5|读作-5绝对值的相反数?
因为+(-5)=-5,+|-5|=,-5<5,
所以+(-5)<+|-5|?
4、?0的绝对值等于0,±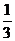 的绝对值等于
的绝对值等于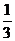 ,没有什么数的绝对值等于-1(为什么?)用符号语言表示应为:
,没有什么数的绝对值等于-1(为什么?)用符号语言表示应为:
|0|=0,|+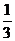 |=
|=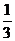 |,|-
|,|-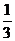 |=
|=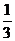 。?
。?
这里应再次强调绝对值是数轴上的点与原点的距离,并指出距离是非负量?
5、?绝对值小于3的数是从-3到3中间的所有的有理数,有无数多个;但绝对值小于3的整数只有五个:-2,-1,0,1,2?
用符号语言表示应为:
因为|x|<3,所以-3<x<3?
如果x是整数,那么x=-2,-1,0,1,2?
6、?由数轴上a、b的位置可以知道a<0,b>0,且|a|<|b|?
所以|a|=-a,|b|=b,
|a+b|=a+b,|b-a|=b-a?
7、?若a+b=0,则a,b互为相反数或a,b都是0,因为绝对值非负,所以只有|a|=0,|b-1|=0,由绝对值意义得a=0,b-1=0?
用符号语言表示应为:
因为|a|+|b-1|=0,所以a=0,b-1=0,
所以a=0,b=1?
启发式教学
现代课堂教学手段
负数大小比较??
3、注意培养学生的推时论证能力?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com