
题目列表(包括答案和解析)
6.若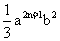 与-5b2a3n-2是同类项,则n=( )
与-5b2a3n-2是同类项,则n=( )
A. 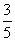 B. -3 C.
B. -3 C. 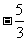 D.3
D.3
5.如果方程6x+3a=22与方程3x+5=11的解相同,那么a= ( )
A. 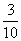 B.
B. 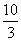 C. -
C. -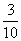 D.-
D.- 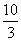 [来源:]
[来源:]
4.如果3x+2=8,那么6x+1= ( )
A. 11 B.26 C.13 D.-11
3.方程4(2-x)-4(x)=60的解是( )
A. 7 B. 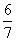 C.-
C.- 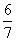 D.-7
D.-7
2. 解方程-3x+5=2x-1, 移项正确的是( )
A.3x-2x=-1+5 B.-3x-2x=5-1
C.3x-2x=-1-5 D.-3x-2x=-1-5
1.解方程6x+1=-4,移项正确的是( )
A. 6x=4-1 B. -6x=-4-1
C.6x=1+4 D.6x=-4-1
3.当a=0,b=0时,方程ax=b有无穷多解(此方程不是一元一次方程).
2.当a=0,b≠0时,方程ax=b无解(此方程不是一元一次方程).
1.当a≠0时,方程ax=b有惟一解x=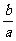 (此时方程为一元一次方程,ax=b(a≠0))是一元一次方程的最简形式.
(此时方程为一元一次方程,ax=b(a≠0))是一元一次方程的最简形式.
[例1]已知关于x的方程kx=4-x的解为正整数,求k所能取得的整数值.
解:关于x的方程kx=4-x的解为正整数.将原方程变形得kx+x=4即(k+1)x=4.因此k+1也为正整数且与x的乘积为4,可得到k+1=4或k+1=2或k+1=1.解得k=3或k=1或k=0.
所以,k可以取得的整数解为0、1、3.
[例2]解方程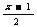 +1=x-1
+1=x-1
解法一:原方程变为
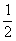 (x-1)+1=x-1.
(x-1)+1=x-1.
去括号,得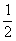 x-
x-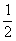 +1=x-1.
+1=x-1.
移项,得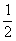 x-x=-1-1+
x-x=-1-1+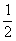 .
.
合并同类项,得-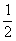 x=-
x=-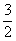 .
.
方程两边同除以-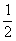 ,得x=3.
,得x=3.
解法二:可以把(x-1)看成一个整体,设(x-1)=A.则原方程变为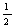 A+1=A
A+1=A
移项,得1=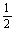 A.
A.
方程两边同除以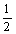 ,得2=A即A=2.
,得2=A即A=2.
解法三:方程两边同乘以2,得
x-1+2=2x-2
移项,得x-2x=-2-2+1
合并同类项,得-x=-3
方程两边同乘以-1,得x=3.
[例3]已知y=-x+b,当x=-1时,y=-1;当x=1时,y的值为多少?
解:由已知,得x=-1时,y=-1可代入y=-x+b中,得-1=-(-1)+b.解得b=-2.所以当x=1时,y=-x+b=-1+(-2)=-3.
由上可知y=-3.
[例4]3a3b2x与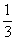 a3b
a3b 是同类项,求出(-x)2003、x2003的值.
是同类项,求出(-x)2003、x2003的值.
解:因为3a3b2x与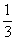 a3b
a3b 是同类项,根据同类项的定义可得2x=4 (x-
是同类项,根据同类项的定义可得2x=4 (x-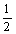 )
)
去括号,得2x=4x-2
移项,得2x-4x=-2
合并同类项得-2x=-2
方程两边同除以-2,得x=1.
将x=1代入
(-x)2003·x2003=(-1)2003·12003=1.
[例5]解方程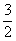 |x+5|=5.
|x+5|=5.
分析:将|x+5|作为一个整体求值,再根据绝对值的定义去掉绝对值符号.
解:由原方程得|x+5|=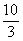 .
.
由绝对值的定义可知
x+5=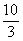 或x+5=-
或x+5=-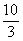 .
.
所以x=-1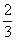 或x=-8
或x=-8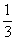 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com