
题目列表(包括答案和解析)
1.下列图形能说明∠1>∠2的是( )

A B C D
49.解析:要求六边形的周长,必须先求出边EF和AF的长.由六边形ABCDEF的六个角都是120°,可知六边形的每一个外角的度数都是60°,如图4,如果延长BA,得到的∠PAF=60°,延长EF,得到的∠PFA=60°,两条直线相交形成三角形APF,在三角形APF中,∠P的度数为180°-60°-60°=60°,因此三角形APF是等边三角形.同样的道理,我们分别延长AB、DC,交于点G,那么三角形BGC为等边三角形.分别延长FE、CD交于点H,则三角形DHE也是等边三角形.所以∠P=∠G=∠H=60°.所以三角形GHP也是等边三角形.于是我们得到三角形APF、三角形BGC、三角形DHE、三角形GHP四个等边三角形.于是就把多边形的问题转化为和等边三角形有关的问题.利用等边三角形的三边相等的性质,可以轻松的求出AF和EF的长,从而求出六边形ABCDEF的周长.
解:如图4,分别作直线AB、CD、EF的延长线使它们交于点G、H、P.
因为六边形ABCDEF的六个角都是120°,
所以六边形ABCDEF的每一个外角的度数都是60°.
所以三角形APF、三角形BGC、三角形DHE、三角形GHP都是等边三角形.
所以GC=BC=8cm,DH=DE=6cm.
所以GH=8+11+6=25cm,FA=PA=PG-AB-BG=25-2-8=15cm,EF=PH-PF-EH=25-15-6=4cm.
所以六边形的周长为2+8+11+6+4+15=46cm.
小结:本题解题的关键是利用多边形和三角形的关系,通过添加辅助线,利用六边形构造出等边三角形,从而利用转化的思想,把多边形问题转化为和三角形有关的问题,利用三角形的性质、定理来解答多边形的问题.
方程思想是我们学习数学的重要思想方法之一.用方程思想求解数学问题时,应从题中的已知量与未知量的关系入手,找出相等关系,运用数学符号语言将相等关系转化为方程,再通过解方程,使问题得到解决.
方程思想应用非常广泛.我们不但能用方程思想解决代数问题,而且还能够解决有关的几何问题.
47.解析:题中告诉了我们按要求拼成.
解:如图:
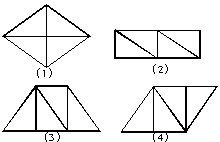
46.解析:我们发现1125°不能被180°整除,所以老师说少加了一个角的度数.我们可设少加的度数为x,利用整除求解.
解:设少加的度数为x.
则1125°=180°×7-135°.
因为0°<x<180°,
所以x=135°.
所以此多边形的内角和为1125°+135°=1260°.
设多边形的边数为n,
则(n-2)×180°=1260°,解得n=9.
所以此多边形是九边形,少加的那个内角的度数是135°.
45.解析:要想BE与DF平行,就要找平行的条件.题中只给出了∠A=∠C=90°,BE平分∠ABC,DF平分∠ADC.那么我们是利用同位角相等呢还是利用同旁内角互补?经过仔细观察图形我们知道∠BFD是三角形ADF的外角,则∠BFD=∠A+∠ADF.而∠ADF是∠ADC的一半,∠ABE是∠ABC的一半,所以我们选择用同旁内角互补来证平行.
解:BE与DF平行.理由如下:
由n边形内角和公式可得四边形内角和为(4-2)×180°=360°.
因为∠A=∠C=90°,
所以∠ADC+∠ABC=180°.
因为BE平分∠ABC,DF平分∠ADC,
所以∠ADF=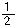 ∠ADC,∠ABE=
∠ADC,∠ABE=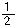 ∠ABC.
∠ABC.
因为∠BFD是三角形ADF的外角,
所以∠BFD=∠A+∠ADF.
所以∠BFD+∠ABE=∠A+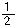 ∠ADC+
∠ADC+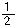 ∠ABC=∠A+
∠ABC=∠A+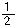 (∠ADC+∠ABC)=90°+90°=180°.
(∠ADC+∠ABC)=90°+90°=180°.
所以BE与DF平行.
44.解析:在第(1)和第(2)问中,没有说明所给边长是腰长还是底边长,因此我们要进行分类讨论.在第(3)问中,只给出了三边长都是整数,而此三角形又是等腰三角形,所以其最长边小于8cm,我们可以用列表法一一列出各组边长.
解:(1)如果腰长为4cm,则底边长为16-4-4=8cm.三边长为4cm,4cm,8cm,不符合三角形三边关系定理.所以应该是底边长为4cm.所以腰长为(16-4)÷2=6cm.三边长为4cm,6cm,6cm,符合三角形三边关系定理,所以另外两边长都为6cm.
(2)如果腰长为6cm,则底边长为16-6-6=4cm.三边长为4cm,6cm,6cm,符合三角形三边关系定理.所以另外两边长分别为6cm和4cm.
如果底边长为6cm,则腰长为(16-6)÷2=5cm.三边长为6cm,5cm,5cm,符合三角形三边关系定理,所以另外两边长都为5cm.
(3)因为周长为16cm,且三边都是整数,所以三角形的最长边不会超过8cm且是等腰三角形,我们可用列表法,求出其各边长如下:
7cm,7cm,2cm;6cm,5cm,5cm;6cm,6cm,4cm,共有这三种情况.
43.解析:本题要求AC与AB的边长的差,且AC与AB的长度都不知道,不少同学感到无从下手.其实,只要我们仔细分析分析题中条件:三角形ABD的周长比三角形ACD的周长小5,即AC-AB+CD-BD=5,又AD是BC边上的中线,所以BD=CD.所以AC-AB=5.
解:AC-AB=5.
42.解析:本题已知一边长和三条高,我们可以利用三角形的面积公式求得另外两边长,三边相加即可得到三角形的周长.
解:由三角形面积公式可得S△ABC=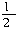 BC×AD=
BC×AD=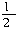 AC×BE,即16×3=4×AC,所以AC=12.
AC×BE,即16×3=4×AC,所以AC=12.
由三角形面积公式可得S△ABC=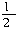 BC×AD=
BC×AD=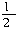 AB×CF,即16×3=6×AB.
AB×CF,即16×3=6×AB.
所以AB=8.
所以三角形ABC的周长为16+12+8=36.
41.解析:利用角平分线的性质解.
解:因为AI、BI、CI为三角形ABC的角平分线,
所以∠BAD=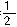 ∠BAC,∠ABI=
∠BAC,∠ABI=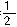 ∠ABC,∠HCI=
∠ABC,∠HCI=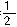 ∠ACB.
∠ACB.
所以∠BAD+∠ABI+∠HCI=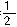 ∠BAC+
∠BAC+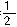 ∠ABC+
∠ABC+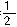 ∠ACB=
∠ACB=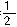 (∠BAC+∠ABC+∠ACB)=
(∠BAC+∠ABC+∠ACB)=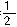 ×180°=90°.
×180°=90°.
所以∠BAD+∠ABI=90°-∠HCI.
又因为∠BAD+∠ABI=∠BID,90°-∠HCI=∠CIH,
所以∠BID=∠CIH.
所以∠BID和∠CIH是相等的关系.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com