6．已知，如图，∠1＝∠2，∠3＝∠4，∠AOF＝.

(1)射线OD是∠AOC的__________；　　　 (2)∠AOC的补角是____________；

(3)_______________是∠AOC的余角；　　 (4)∠DOC的余角是____________；

(5)∠COF的补角____________.

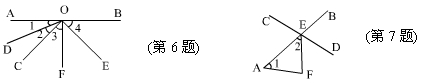
5．讲台上放着一个圆锥和一个正方体(如图)请说明下面的三幅图分别是从哪个方向看到的。

(1)从　　　　 面看到的平面图形；(2)从　　　　 面看到的平面图形；(3)从　　 面看到的平面图形。　

4．如图，该图中不同的线段共有_______条.

3．请同学们手拿一枚硬币，将其立在桌面上用力一转，

它形成的是一个　　　 体,由此说明________________.

2．圆柱的侧面展开图是一个　　　　　 ，圆锥的侧面展开图是一个　　　　　　 ，棱柱的侧面展开图是一个　　　　　　　 。

1．正方体有______条棱，_____个顶点，　　　 个面.

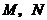23．(12分)(1)如下图，已知点在线段上，且，，点分别是，的中点，求线段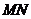的的长度．

(2)在(1)中，如果，，其它条件不变，你能猜出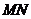的长度吗？请你用一句简洁的话表述你发现的规律．

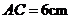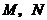(3)对于(1)题，如果我们这样叙述它：“已知线段，，点在直线上，点分别是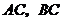的中点，求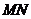的长度．”结果会有变化吗？如果有，求出结果．

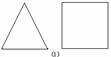
22．(9分)如图，BO、CO分别平分∠ABC和∠ACB，

(1)若∠A = 60°，求∠BOC；

(2)若∠A =100°、120°，∠BOC又是多少？

　 (3)由(1)、(2)你又发现了什么规律？当∠A的度数发生变化后，你的结论仍成立吗？

　 (提示：三角形的内角和等于180°)

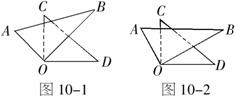
21.(6分)把一副三角尺的直角顶点重叠在一起．

(1)如图10－1，当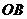平分时，则和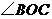的和是多少度？

(2)如图10－2，当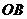不平分时，则和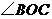的和是多少度？

20. (6分)知识是用来为人类服务的，我们应该把它们用于有意义的方．下面就两个情景请你作出评判．

情景一：从教室到图书馆，总有少数同学不走人行道而横穿草坪，这是为什么呢？试用所学数学知识来说明这个问题。

情景二：A、B是河流l两旁的两个村庄，现要在河边修一个抽水站向两村供水，问抽水站修在什么地方才能使所需的管道最短？请在图中表示出抽水站点P的位置，并说明你的理由：　　　 　　　　　　　　　　　　　　　　　　　　

你赞同以上哪种做法？你认为应用数学知识为人类服务时应注意什么？