7.(1)4+8+10+16+10=50名；(2)12；

8(1)100户，(2)用水量不足10吨的有55户，用水量超过16吨的有10户；

(3)44000户；

1.C；2.D；3. (1)24O　 O.8%　 (2)2∶4∶9∶6∶3　 (3)6O　 25%；4.45%；5.(1)48，(2)12，0.25

6解：(1)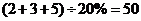(人)

(2)如图所示．

(3)85~100分：，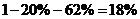

所以，含有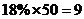(人)

9.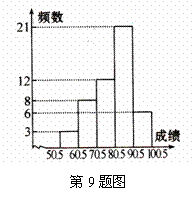某校七年级共500名学生参加法律知识测试，从中随机抽取一部分试卷成绩，作统计分析，进行整理后分成五组，并绘制成频数分布直方图，请你结合直方图提供的信息，解答以下问题：

(1)随机抽取了多少名学生的测试成绩？

(2)70.5-80.5分这一分数段的频率是多少？

(3)箬90分以上(不含90分)定为优秀，

则样本的优秀率是多少？

(4)请你估计该校七年级这次法律知识测试

获得优秀大约有多少人？

课时一答案：

7.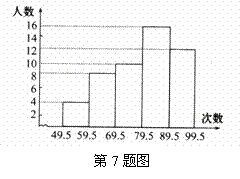对某班学生一次数学测验中成绩进行统计分析，各分数段的人数如图(分数取正整数)，请观察图形，并回答下列问题：

(1)该班有多少名学生？

(2)89.5-99.5这一组的频数是多少？

8为了了解居民月用水，某市对居民用水进行了抽样调查，并制成如下直方图.

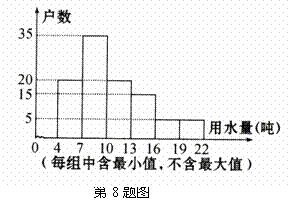(1)这次抽查一共抽查了多少户？

(2)用水量不足10吨的有多少户？

用水量超过16吨的有多少户？

(3)假设该区有8万户居民，

估计用水量不超过10吨的有多少户？

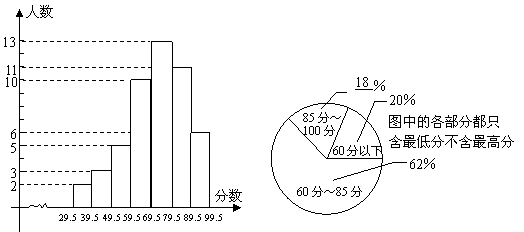
6. 七年级一班的两位学生对本班的一次数学成绩(分数取整数，满分为100分)进行了一次初步统计，看到80分以上(含80分)有17人，但没有满分，也没有低于30分的．为更清楚了解本班的考试情况，他们分别用两种方式进行了统计分析，如图1和图2所示．请根据图中提供的信息回答下列问题：

(1)班级共有多少名学生参加了考试？

(2)填上两个图中三个空缺的部分；

(3)问85分到89分的学生有多少人？

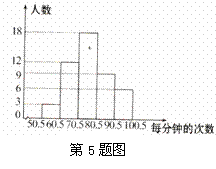
5.某中学将踢踺子作为趣味运动会的一个比赛项目，

七年纪(6)班同学进行了选拔测试，将所测成绩

进行整理，分成五组，并绘制成频数分布直方图

(如图所示).请结合直方图土的信息，回答下列问题：

(1)该班　　　 名学生参加这次测试？

(2)60.5-70.5这一分数段的频数为　　　 ，

频率为　　　

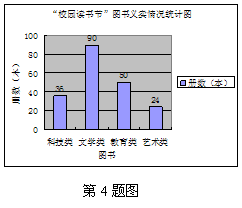
4. 在“校园读书节”期间，学生会组织了一次图书义卖活动，提供了四种类别的图书，下

图是本次义卖情况统计图，则这次活动共卖出的文学类图书本数占所有卖出本数的百分比是＿＿＿＿＿。

2.有关频数分布表和频数分布直方图的理解，正确的是(　　 )

A.频数分布表能清楚地反映数据的变化情况

B.频数分布直方图能清楚地反映数据的变化情况

C.频数分布直方图能清楚地表示出各部分在总体中所占的百分比

D.二者均不能清楚地反映数据的变化情况和在总体中所占的百分比，但能反映出每个项目的具体数目

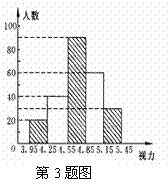
3 初中生的视力状况受到全社会的广泛关注，某市有关部门对全市3万名初中生视力状况进行了一次抽样调查，图12-17是利用所得数据绘制的频数分布直方图(长方形的高表示该组人数)，根据图中所提供的信息，回答下列问题.

(1)本次调查共抽测了　　　　 名学生，占该市初中生总数的百分比是　　　　 ；

(2)从左到右五个小组的频率之比是　　　　 ；

(3)如果视力在4.9-5.1(含4.9，5.1)均属正常，则全市有　　　 名初中生的视力正常，视力正常的合格率是　　　 .

1.在频数分布直方图中，每个小长方形的面积等于(　　　 )

A组距　　　 B.组数　　 C.每个组频数　　　 D. 每个组频率

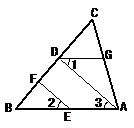
23．如图，EF∥AD，∠1 =∠2，∠BAC = 70°。将求∠AGD的过程填写完整。

因为EF∥AD，所以 ∠2 = 　　　　　。又因为 ∠1 = ∠2，所以 ∠1 = ∠3。 所以AB∥　　　　 。所以∠BAC + 　　　　　　= 180°。又因为∠BAC = 70°，所以∠AGD =　　　　　 。