
题目列表(包括答案和解析)
12.解:原式=3(x2+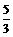 x)-2
x)-2
=3(x2+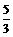 x+
x+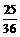 -
-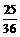 )-2 *
)-2 *
=3(x+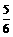 )2-3×
)2-3×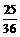 -2
-2
=3(x+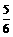 )2-
)2-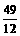
=3[(x+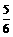 )2-
)2-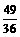 ]
]
=3(x+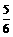 +
+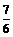 )(x+
)(x+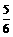 -
-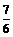 )
)
=3(x+2)(x-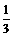 )
)
=(x+2)(3x-1)
提示:*这步很重要,根据完全平方式的结构配出来的。对于任意二次三项式ax2+bx+c(a≠0)可配成a(x+ )2+
)2+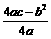 .
.
11.解:原式=x2-2x+1-1-8 *
=(x-1)2-32
=(x-1+3)(x-1-3)
= (x+2)(x-4)
提示:本题用了配方法,将x2-2x加上1个“1”又减了一个“1”,从而构成完全平方式。
10.解:原式=(a2+b2 +2ab)+2bc+2ac+c2
=(a+b)2+2(a+b)c+c2
=(a+b+c)2
提示:*将(a+b)视为 1个整体。
9. 解:原式= (x+y)2(x2-12x+36)-(x+y)4
=(x+y)2[(x-6)2-(x+y)2]
=(x+y)2(x-6+x+y)(x-6-x-y)
=(x+y)2(2x+y-6)(-6-y)
= - (x+y)2(2x+y-6)(y+6)
8. 解:原式=y2[(x+y)2-12(x+y)+36]-y4
=y2(x+y-6)2-y4
=y2[(x+y-6)2-y2]
=y2(x+y-6+y)(x+y-6-y)
= y2(x+2y-6)(x-6)
7. 解: 原式= x4-x3-(x-1)
= x3(x-1)-(x-1)
=(x-1)(x3-1)
=(x-1)2(x2+x+1)
提示:通常四项或者以上的因式分解,分组分的要合适,否则无法分解。另外,本题的结果不可写成(x-1)(x-1)( x2+x+1),能写成乘方的形式的,一定要写成乘方的形式。*使用了立方差公式,x3-1=(x-1)( x2+x+1)
6.解:原式=-(a2-2ab+b2-4)
=-(a-b+2)(a-b-2)
提示:如果多项式的第一项是负的,一般要提出负号,使括号内第一项系数是正的。但也不能见负号就先“提”,要对全题进行分析.防止出现诸如-9x2+4y2=(-3x)2-(2y)2=(-3x+2y)(-3x-2y)=(3x-2y)(3x+2y)的错误。
5.解:原式=( x2+1)( x2-1)
=( x2+1)(x+1)(x-1)
提示:许多同学分解到(x2+1)( x2-1)就不再分解了,因式分解必须分解到不能再分解为止。
4.解:原式= [(a+b)x]2-2(a+b)(a-b)xy+[(a-b)y]2
=(ax+bx-ay+by)2[
提示:将(a+b)x和(a-b)y视为 一个整体。
3.解:原式=3a(b-1)(1-8a3)
=3a(b-1)(1-2a)(1+2a+4a2)
提示:立方差公式:a3-b3=(a-b)( a2+ab+b2)
立方和公式:a3+ b3=(a+b)( a2-ab+b2)
所以,1-8 a3=(1-2a)(1+2a+4a2)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com