3、已知一个圆，任意画出它的三条半径，能得到(　 )个扇形.

　 A、4　　　 B、5　　　　 C、6　　 　D、8

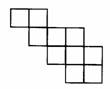
2、如图1–37，图中共有正方形(　　 )　　　　　　　　　

　 A、12个　　 B、13个　　 C、15个　　 D、18个　　　　　　

1、用各种不同的方法把图形分割成三角形，至少可以分割成5个三角形的多边形是(　 )

　 A、五边形　　 B、六边形　　 C、七边形　　 D、八边形　　　

10.(1)如图5-1-15(1)所示，两条直线AB与CD相交成几对对顶角？

(2)如图5-1-15(2)所示,三条直线AB、CD、EF相交呢？

(3)试猜想n条直线相交会成多少对对顶角？

图5-1-15

解:(1)两条直线AB与CD相交成2对对?顶角.

(2)三条直线AB、CD、EF相交有6对对顶角.

(3)因为3条不同直线相交所成的对顶角有(3×2)÷2×2=6(对)；4条不同直线相交所成的对顶角有(4×3)÷2×2=12(对)；则可推测：n条直线相交所成的对顶角有n×(n-1)÷2×2=n(n-1)(对).

9.如图5-1-14,一棵小树生长时与地面成80°角，它的主根深入泥土，如果主根和小树在同一条直线上，那么∠2等于多少度？

图5-1-14

解:∵∠1+80°=90°，∴∠1=10°.

∵∠1=∠2(对顶角相等)，∴∠2=10°.

8.图5-1-13中的∠1和∠2,∠3和∠4分别是由哪两条直线被哪一条直线所截而成的?它们各是什么角?

图5-1-13

解:由题图(1)知∠1和∠2的公共边所在的直线是BD,则BD是截线,所以∠1和∠2是由直线AB,CD被直线BD所截而形成的内错角;∠3和∠4的公共边所在的直线是BD,则BD是截线,所以∠3和∠4是由直线AD,BC被直线BD所截而形成的内错角.由题图(2)知,∠1和∠2的公共边所在的直线是BC,则BC是截线,所以∠1和∠2是由直线AB,CD被直线BC所截而形成的同旁内角;∠3和∠4的公共边所在的直线是AB,则AB是截线,所以∠3和∠4是由直线AD,BC被直线AB所截而形成的同位角.

7.如图5-1-12,直线AB、CD、EF相交于点O.

图5-1-12

(1)写出∠AOD、∠EOC的对顶角;

(2)已知∠AOC=50°,求∠BOD、∠COB的度数.

解:(1)∠AOD的对顶角是∠COB;∠EOC的对顶角是∠DOF.

(2)∠BOD=∠AOC=50°(对顶角相等),

∠COB=180-∠AOC=180°-50°=130°(邻补角的定义).

6.A、B两厂在公路同侧,拟在公路边建一货场C,若由B厂独家兴建,并考虑B厂的利益,则要求货物离B厂最近,请在图5-1-11中作出此时货场C的位置,并说出这样做的道理.

图5-1-11

解:如图所示,过B作公路所在直线的垂线,垂足O就是所求货场C的位置.

理由:根据“垂线段最短”,所以BO是点B到公路的最短线段.

5.如图5-1-10,直线AB、CD相交于O,作∠DOE=∠BOD,OF平分∠AOE,∠AOC=28°,求∠EOF的度数.

图5-1-10

解:由题知∠BOD=∠AOC=28°(对顶角相等),

因为∠DOE=∠BOD,所以∠BOE=2∠BOD=56°.

因为∠AOE+∠BOE=180°,

所以∠AOE=124°.

因为OF平分∠AOE,

所以∠EOF=∠AOE=62°.

4.如图5-1-9所示,直线AB、CD相交于O点,∠AOD=130°,则∠BOC=______________, ∠AOC=______________,∠BOD=______________.

解析:利用对顶角相等和邻补角的关系求解.

答案:130°　 50°　 50°