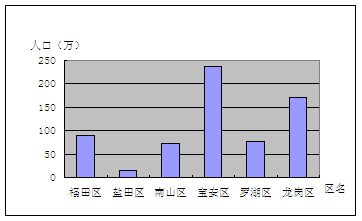
2．到2000年，深圳市特区内、外总人口达到698万。其中福田区90万，南山区72万，盐田区15万，保安区273万，罗湖区77万，龙岗区171万

根据以上数据制作统计表。

用什么统计图可直观地描述各区的人口情况。

解析：(1)问较简单，(2)问要描述各区的人口情况从绝对人口数或各区人口数所占的百分比均可直观地描述。所以用条形统计图或扇形统计图均可。

解：(1)

(2)

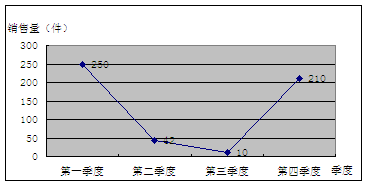
1．小明开了一家皮装专卖店，2005年各月份的销售情况如下表：

用合适的统计图表示2005年各季度的销售量变化情况。

解析：由于求各季度的销售量变化情况根据三种统计图的特点选择折线统计图较合适。

解：

5.3统计图的选择同步练习

14.在△ABC中，已知∠A=55°，高BD、CE交于点O，且点O不与点B、C重合，求∠BOC的度数.

答案：(1)若△ABC是锐角三角形，

如图所示.

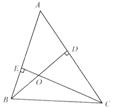
因为CE，BD是△ABC的两条高，所以∠CEB=90°，∠BDA=90°(三角形的高的定义).

所以∠A=180°-90°-∠ABO=90°-∠ABO(三角形的内角和定理)，∠EOD=180°-90°-∠ABO=90°-∠ABO(三角形的内角和定理).

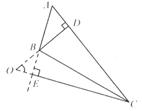
第14题图

所以∠A=∠EOB(等量代换).

又∠EOB+∠BOC=180°(邻补角定义)，

所以∠A+∠BOC=180(等量代换).又∠A=55°(已知)，

所以∠BOC=180°-∠A=180°-55°=125°.

(2)若△ABC是钝角三角形，如图7-48所示.

因为∠BDA=90°，∠BEO=90°，

所以∠BOC=180°-90°-∠EBO=90°-∠EBO(三角形的内角和定理)，∠A=180°-90°-∠ABD-90°-∠ABD

(三角形的内角和定理).

又∠ABD=∠EBO(对顶角相等)，∠A=55°(已知)，

所以∠BOC=∠A=55°(等量代换)。

13.△ABC中，AD、AE分别是高和角的平分线，∠B=70°，∠C=40°，求∠DAF的度数.

答案：∠DAE=∠BAE-∠BAD=15°

12.(2010广西)如图7-44所示，则△ABC的形状是(　　 )

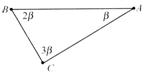
图7-44

A.锐角三角形　　　　　　　　　　　　 B.钝角三角形

C.直角三角形　　　　　　　　　　　　 D.等腰三角形

答案：C(点拨：草坪面积是三个长方形面积和以三角形的三个顶点为圆心的三个扇形面积之和)

模拟在线

11.(江苏)如图7-43，在△ABC中，D、E分别是AB、AC边上的点，DE∥BC，∠ADE=30°，∠C=120°，则∠A=(　　 )

A.60°　　　　　 　D.45°　　　　　　 C.30°　　　　　 D.20°

图7-41　　　　　 图7-42　　　　　 图7-43

答案：C

10.如图7-42，∠ABO=20°，∠ACO=40°，∠BOC=2∠A，则∠A=__________.

答案：60°

9.如图7-41，∠A+∠B+∠C+∠D+∠E+∠F=___________.

答案：360°

8.直角三角形两锐角平分线相交所成的角的度数是____________.

答案：45°或135°