6.一个多边形除去一个内角外，其余各角之和为2 750°,求这个多边形的边数及去掉的角的度数.

解析：由于多边形的内角和是180°的整数倍，所以去掉的这个角与2 750°÷180的余数的和应是180°.

设去掉的这个角为α,又有2 750°÷180的余数为50°，所以可得α+50°=180°.

所以α=130°.∴该多边形的边数为(2 750°+130°)÷180°+2=18.

所以这个多边形的边数为18，去掉的角度为130°.

30分钟训练(巩固类训练，可用于课后)

5.已知多边形的每一个内角都是150°，求它的边数和内角和.

解：设这个多边形为n边形，则(n-2)180°=n·150°，

所以n=12.所以(12-2)×180°=1 800°.

答：它的边数为12，内角和为1 800°.

4.过n边形一个顶点可作_______________条对角线，过n个顶点可作_______________条对角线.

解析：由图形规律可得，过n边形的一个顶点可作(n-3)条对角线，则过n个顶点可作(n-3)·n÷2,即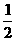n(n-3)条.

答案：n-3　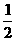 n(n-3)

3.凸n边形的n个内角与某一个外角的和为1 350°，则n等于(　　 )

A.6　　　　　　　　 B.7　　　　　　　　 C.8　　　　　　　　　　 D.9

解析：设该外角为α，则(1 350°-α)应是180°的整数倍，所以1 350°÷180°的整数部分即n边形的边数.

答案：D

2.若正n边形的一个外角为60°，则n为(　　 )

A.4　　　　　　 　　B.5　　　　　　　　 C.6　　　　　　　　　　 D.9

解析：n边形的外角和为360°，由于正n边形的一个外角为60°，所以n=360°÷60°=6.

答案：C

1.若一个多边形的边数减少1，则它的内角和(　　 )

A.不变　　　　　　　　　　　　　　　　 B.增加180°

C.减少180°　　　　　　　　　　　　　　 D.无法确定

解析：因为(n-2)180°-(n-1-2)180°=180°，所以应选C.

答案：C

4.过多边形一个顶点可引5条对角线，那么这个多边形是______________边形.(　　 )

A.5　　　　　　　　 B.7　　　　　　　　 C.8　　　　　　　　　　 D.10

解析：过n边形的一个顶点可作(n-3)条对角线，则n-3=5,∴n=8.

答案：C

10分钟训练(强化类训练，可用于课中)

3.如果一个多边形的内角和为1 440°，那么这个多边形是(　　 )

A.6边形　　　　　　 B.8边形　　　　　　 C.10边形　　　　　　　 D.12边形

解析：设这个多边形为n边形，由n边形的内角和定理得(n-2)180°=1 440°，解得n=10.

答案：C

2.n边形的内角和等于_____________度，外角和等于_____________度.

解析：n边形的内角和等于(n-2)180°，外角和等于360°.

答案：(n-2)180　 360

1.三角形的内角和等于_____________度，外角和等于_____________度.

解析：三角形的内角和等于180°，外角和等于360°.

答案：180　 360