4.如图7-2-4所示，∠1+∠2+∠3+∠4=_______________.

图7-2-4

解析：利用外角的知识把这些角转到同一个三角形中，过程如下：因为∠2+∠3=∠5，所以∠1+∠2+∠3+∠4=∠1+∠5+∠4=180°.也可以把这些角转到另一个三角形中，过程如下：因为∠1+∠4=∠6，所以∠1+?∠2+∠3+∠4=∠6+∠2+∠3=180°.

答案：180°

3.在△ABC中，∠A-∠C=25°,∠B-∠A=10°,则∠B=___________.

解析：由题意得∠A=∠B-10°,∠C=∠A-25°,∴∠C=∠B-10°-25°.根据三角形的内角和为180°，∴∠A+∠B+∠C=180°.

∴∠B-10°+∠B+∠B-10°-25°=180°.∴∠B=75°.

答案：75°

2.三角形的一个外角等于与它相邻内角的4倍，等于与它不相邻的一个内角的2倍，则该三角形的各角的度数是(　　 )

A.45°，45°，90°　　　　　　　　　　　 B.30°，60°，90°

C.36°，72°，72°　　　　　　　　　　　 D.25°，25°，130°

解析：设与这个外角相邻的内角为x，则x+4x=180°，∴x=36°.∴另外两个内角中有一个角为=72°.

∴第三个内角为180°-36°-72°=72°.

答案：C

1.下列说法正确的是(　　 )

A.在一个三角形中最多有两个锐角　　　　　 B.在一个三角形中最多有两个钝角

C.在一个三角形中最多有两个直角　　　　　 D.在一个三角形中最少有两个锐角

解析：根据“三角形的内角和等于180°”来判断.当一个三角形中有两个钝角或直角时，一个三角形的内角和要超过180°,所以在一个三角形中最多有一个钝角或直角，至少有两个锐角，也可以三个角都是锐角.

答案：D

4.如图7-2-3所示，已知∠A=60°，∠B=45°，可知∠α的度数吗？

图7-2-3

解析：依据“三角形的一个外角等于和它不相邻的两个内角的和”可得∠α=∠A+∠B=60°+45°=105°.

答案：105°.

10分钟训练(强化类训练，可用于课中)

3.在△ABC中，∠C=90°，∠A=30°，则∠B=_____________.

解析：由三角形的内角和等于180°，可得∠B=180°-∠A-∠C=180°-30°-90°=60°.

答案：60°

2.填空：已知△ABC．求证：∠A+∠B+∠C=180°．

证明：如图7-2-2，延长线段AB到D，过点B画BE∥AC．

图7-2-2

因为BE∥AC，

所以∠A=∠EBD(　　　　　　　　　　　　　　 )，

∠C=∠CBE(　　　　　　　　　　　　　 ).

又因为∠ABC+∠CBE+∠EBD=180°(　　　　　　　　　　　　 )，

所以∠A+∠ABC+∠C=180°．

解析：根据平行线的性质以及平角的定义可得.

答案：两条直线平行，同位角相等　 两条直线平行，内错角相等　 平角的定义

1.如图7-2-1,∠ACB=90°,CD⊥AB,垂足为D，下列结论错误的是(　　 )

图7-2-1

A.图中有三个直角三角形　　　　　　　　　 B.∠1=∠2

C.∠1和∠B都是∠A的余角　　　　　　　 D.∠2=∠A

解析：∵∠ACB=90°,CD⊥AB,

∴图中有三个直角三角形.

∴∠1+∠2=90°，∠1+∠A=90°,∠2+∠B=90°,∠A+∠B=90°.

∴∠2=∠A,∠1=∠B.

但是∠1不一定等于∠2.

答案：B

7.2　 与三角形有关的角

5分钟训练(预习类训练，可用于课前)

11.已知一个多边形的对角线条数是边数的3倍，求它的内角和.

解：设这个多边形的边数为n，n边形的对角线为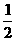n(n-3)条，根据题意列方程，得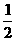n(n-3)=3n,

即n(n-3)=6n.

∵n≠0,两边都除以n，得n-3=6,

∴n=9.

从而它的内角和为(n-2)·180°=(9-2)×180°=1 260°.

答：这个多边形的内角和为1 260°.