3.如图7-1-3所示，已知AD、BE、CF分别是△ABC的高、中线和角平分线，则∠___________=∠___________=90°；___________=___________=；∠___________=∠___________=∠___________.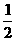

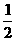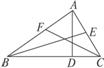
图7-1-3

解析：直接依据三角形的高、中线、角平分线的定义可得.

答案：ADB　 ADC　 AE　 CE　 AC　 ACF　 BCF　 ACB

2.如图7-1-2所示，已知在△ABC中，BC边上的高为(　　 )

图7-1-2

A.BE 　　　　　　　　B.BF　　　　　　 C.AD　　　　　　　 D.CF

解析：BC边上的高是由顶点A向BC所在直线作垂线而成的，所以AD才是BC边上?的高.

答案：C

1.四条线段的长分别为2、3、4、5，从中选出三条组成三角形的个数共有(　　 )

A.2个　　　　　　　 B.3个　　　　　　 C.4个　　　 　　　　D.5个

解析：我们可分别从中取出三条线段作为三角形的三条边，然后再依据“三角形三边之间的不等关系”判断这三个数能否构成三角形.过程如下表：

答案：B

4.三角形的三边之间的关系是_______________.其理论依据是_____________.

解析：如图，把AB+AC与BC看作是B、C两点之间的连线.根据“两点之间的所有连线中线段最短”可得AB+AC＞BC.

答案：三角形的任意两边之和大于第三边

两点之间的所有连线中线段最短

10分钟训练(强化类训练，可用于课中)

3.三角形的木架不易变形的原因是________________.

答案：三角形具有稳定性

2.三角形的角平分线、中线、高线中(　　 )

A.每一条都是线段　　　　　　　　　　　 B.角平分线是射线，其余是线段

C.高线是直线，其余是线段　　　　　　　 D.高线是直线，角平分线是射线，中线是线段

解析：由三角形的角平分线、中线、高线的定义可知，三角形的角平分线、中线、高线都是线段.

答案：A

1.如图7-1-1所示，图中三角形的个数是(　　 )

图7-1-1

A.2　　　　　　　　 B.3　　　　　　　　 C.4　　　　　　　　 D.5

解析：根据三角形的定义，不在同一条直线上的三条线段首尾顺次相接组成的图形叫三角形.此题容易受到忽略的三角形是：△ACE、△BDE、△ABE，容易把以A、B、E为顶点的内角分别表示为∠A、∠B、∠E；此外,此题还应该做到对三角形个数的不重不漏.

答案：D

7.1　 与三角形有关的线段

5分钟训练(预习类训练，可用于课前)

10.如图7-2-12，BC⊥ED，垂足为O，∠A=27°，∠D=20°，求∠ACB与∠B的度数.

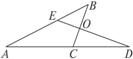
图7-2-12

分析：已知∠D=20°，∠COD=90°，∴利用三角形的内角与外角的关系可以求出∠ACB，再利用三角形的内角和定理可求得∠B.

解：∵BC⊥ED，∴∠COD=90°.又∵∠D=20°，∴∠ACB=∠COD+∠D=110°(三角形的外角等于与它不相邻的两个内角的和).

∵∠A+∠B+∠ACB=180°(三角形的内角和是180°)，∴∠B=180°-27°-110°=43°.

9.如果三角形的三个外角的比为3∶4∶5，那么这个三角形是什么形状的三角形？试说明理由.

解：三角形是直角三角形.

理由：因为三角形三个外角之比为3∶4∶5，所以可设三个外角分别为3x°、4x°、5x°，根据三角形的外角和等于360°可得3x+4x+5x=360,解得x=30,所以三个外角分别为90°、120°、150°.

所以与之对应的三个内角分别为90°、60°、30°.故原三角形为直角三角形.