6.已知线段a、b、c且a＜b＜c,则以a、b、c为边可组成三角形的条件是______________.

解析：直接利用三角形三边关系的简便的判定方法--“较小的两条线段之和大于最大的线段”，便可构成三角形.

答案：a+b＞c

5.如图7-1-5所示，在图(1)中，互不重叠的三角形共有4个，在图(2)中，互不重叠的三角形共有7个，在图(3)中，互不重叠的三角形共有10个，…，则在第n个图形中，互不重叠的三角形共有_____________个.(用含n的代数式表示)

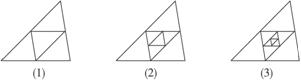
图7-1-5

解析：我们通过观察图形可以发现：在图(1)中有3+1=4个三角形，在图(2)中有3+3+1=7个三角形，在图(3)中有3+3+3+1=10个三角形，所以依此类推，在第n个图形中应有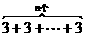+1=3n+1个三角形.

答案：3n+1

4.用7根火柴首尾顺次连结摆成一个三角形，能摆成不同的三角形的个数是______________.

解析：由题意可设三角形的周长为7，且三边均为整数，根据三角形的三边关系可确定，只能摆成3，3，1与2，2，3两个不同的三角形.

答案：2

3.等腰三角形底边长为5厘米，一腰上的中线把其周长分成差为3厘米的两部分，则腰长为______________.

解析：如图所示，应分两种情况，设AB=2x,则AD=CD=x,第一种情况:当△ABD比△BCD的周长大3厘米时，可列方程为(2x+x+BD)-(5+x+BD)=3,所以解得x=4.此时△ABC三边分别为8厘米、8厘米、5厘米，可以构成三角形.第二种情况:当△BCD比△ABD的周长大3厘米时，可列方程为(5+x+BD)-(2x+x+BD)=3,所以解得x=1，此时△ABC三边分别为2厘米、2厘米、5厘米，由于2厘米+2厘米＜5厘米，所以不能构成三角形.

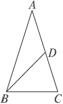
答案：8厘米

2.(2010黑龙江佳木斯模拟，15)一个三角形的两条边长分别为3和7，且第三边长为整数，这样的三角形的周长最小值是(　　 )

A.14　　　　　　　 B.15　　　　　　　 C.16　　　　　　　　　 D.17

解析：根据“三角形的任意两边之和大于第三边”，可得“三角形的任意两边之差小于第三边”，所以第三边的取值范围是“7-3＜第三边＜7+3”.所以第三边应可以是5，6，7，8或9.所以三角形周长的最小值为3+7+5=15.

答案：B

1.下列各组数分别表示三条线段的长度，能组成三角形的是(　　 )

A.2，4，6　　　　　　　　　　　　　　 B.3x，5x，7x

C.4，5，11　　　　　　　　　　　　　 D.三边的比是1∶2∶4

解析：在选项A中，2+4=6，所以该组线段不能组成三角形；在选项B中，3x+5x=8x＞7x，所以该组线段能组成三角形；在选项C中，5+4=9＜11，所以该组线段不能组成三角形；在选项D中，设最小边为a,则有a+2a=3a＜4a，所以该组线段不能组成三角形.

答案：B

7.下面每组数分别是三根小木棒的长度，用它们能摆成三角形吗？实际摆一摆，验证你的结论.

(1)3 cm,4 cm,5 cm；(2)8 cm,7 cm,15 cm；(3)13 cm,12 cm,20 cm；(4)5 cm,5 cm,11 cm.

解：(1)因为3+4＞5,所以3 cm,4 cm,5 cm能摆成三角形.

(2)因为8+7=15,所以8 cm,7 cm,?15 cm不能摆成三角形.

(3)因为13+12＞20,所以13 cm,12 cm,20 cm能摆成三角形.

(4)因为5+5＜11,所以5 cm,5 cm,?11 cm不能摆成三角形.

30分钟训练(巩固类训练，可用于课后)

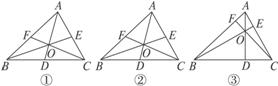
6.(1)在图7-1-4①中，画出三角形的三条角平分线，并观察它们的交点；

(2)在图7-1-4②中，画出三角形的三条中线，并观察它们的交点；

(3)在图7-1-4③中，画出三角形的三条高，并观察它们的交点.

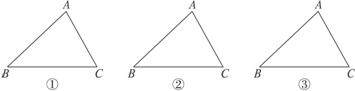
图7-1-4

解：(1)根据三角形角平分线的定义，画出∠A的平分线并且与对边BC交于点D，所以AD即为三角形的角平分线.同理，也可画出BE和CF，可以发现AD、BE、CF都交于点O,如图①所示.

(2)根据三角形中线的定义，先找出BC边的中点D，再连结AD即可，同理也可画出BE和CF，可以发现AD、BE、CF都交于点O,如图②所示.

(3)根据三角形高的定义，先画AD⊥BC于D，所以线段AD即为三角形的高，同理也可画出BE和CF，可以发现AD、BE、CF都交于点O，如图③所示.

5.以4 cm长的线段为底，1 cm长的线段为腰，能否组成一个等腰三角形？如果以4 cm长的线段为底组成一个等腰三角形，腰长应在什么范围内？

解：对于第(1)问：先假设这三条线段能组成一个等腰三角形，则这个三角形的三边分别为4 cm、1 cm、1 cm,但是1 cm+1 cm＜4 cm,即较小两边的和小于最大边，所以它们不能组成三角形.故以4 cm长的线段为底，1 cm长的线段为腰，不能组成一个等腰三角形.对于第(2)问：我们可以采用列不等式的方法，设等腰三角形的腰长为x cm,则三角形的三边分别为4 cm、x cm、x cm,于是可列不等式为x cm+x cm＞4 cm,即x＞2.故以4 cm长的线段为底所组成等腰三角形，腰长的范围应是x＞2.

4.若一个三角形三边长为3厘米、7厘米、x厘米，则x的取值范围为___________，此三角形的周长l(厘米)的取值范围为___________.

解析：此题我们可以比较容易地根据“三角形三边的关系”列出不等式：7-3＜x＜7+3，所以x的取值范围可求；从而周长l的取值范围可列不等式为3+7+4＜l＜3+7+10.

答案：4＜x＜10　 14＜l＜20