
题目列表(包括答案和解析)
2.如图9-3-1,不等式组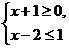 的解集在数轴上的表示正确的是( )
的解集在数轴上的表示正确的是( )

图9-3-1
解析:选项A的解集是x≥3,选项B的解集是x≤-1,选项C的解集是空集,选项D的解集是-1≤x≤3,而原不等式组的解集是?-1≤x≤3.
答案:D
1.(2010重庆模拟,5)不等式组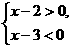 的解集是( )
的解集是( )
A.x>2 B.x<3 C.2<x<3 D.无解
解析:解两个不等式,得x>2且x<3,所以其解集为2<x<3.
答案:C
3.填空:(1)若a>b,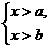 的解集为________________.
的解集为________________.
(2)若a>b,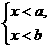 的解集为_______________.
的解集为_______________.
(3)若a>b,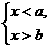 的解集为_______________.
的解集为_______________.
(4)若a>b,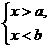 的解集为_______________.
的解集为_______________.
解析:根据“同大取大,同小取小,不大不小中间找,大大小小没得找”来解决.
答案:(1)x>a (2)x<b (3)b<x<a ?(4)无解
10分钟训练(强化类训练,可用于课中)
2.不等式组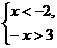 的解集是( )
的解集是( )
A.x<-3 B.x<-2 C.-3<x<-2 D.x<-3或x<-2
解析:求出两个不等式的解集的公共部分.
答案:A
1.下列各式中是一元一次不等式组的是( )
A.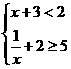 B.
B.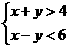
C.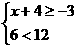 D.
D.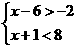
解析:选项A中第二个不等式不是一元二次不等式,选项B中两个不等式中含有两个未知数,选项C中6<12不是一元一次不等式,所以选项A、B、C都不正确.只有选项D符合一元一次不等式组的要求.
答案:D
9.3 一元一次不等式组
5分钟训练(预习类训练,可用于课前)
10.有A、B、C、D、E五个队分在同一个小组进行单循环赛篮球比赛,争夺出线权,比赛规则规定;胜一场得3分,平一场得1分,负一场得0分,小组中名次在前的两个队出线,小组赛结束后,A队的积分为9分.
(1)A队的战绩是几胜几负几平?
(2)如果小组中有一个队的战绩为全胜,A队能否出线?
(3)如果小组中有一个队的积分为10分,A队能否出线?
(4)如果小组中积分最高的队积9分,A队能否出线?
解:因为这五个队进行单循环比赛,每队都比赛4场,所以总场数为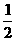 ×5×4=10(场).
×5×4=10(场).
根据比赛的规则,得每场结果分出胜负,两队得分和为3分;每场结果为平局的比赛,每队各得1分,两队得分和为2分.因此,这10场比赛若都分出胜负,则各队积分总和最大为30分;若都赛成平局,则各队积分总和最小为20分.
(1)设A队胜X场,平Y场,则负(4-X-Y)场.
∴3X+Y+0×(4-X-Y)=9,
即3X+Y=9,
∴Y=9-3X.
∵0≤X≤4,
∴当整数X=0,1,2,3,4时,Y=9,6,3,0,-3.
又∵0≤Y≤4且0≤X+Y≤4,
∴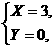
即A队积9分时,胜3场,负1场.
(2)若有一队战绩为全胜,则不妨设这个队为B队,这时,B队胜4场,积12分,它名列小组第一,A队能否出线取决于C、D、E三队中是否有积分多于或等于9分的队.
又∵10场比赛积分最大为30分,去掉A、B两队的积分,C、D、E三队共积9分,
∴C、D、E三队积分都小于9分,所以?A队一定出线.
(3)如果小组中有一队积分为10分,不妨设为B队,
设B队胜X场,平Y场,则负(4-X-Y)场.
∴3X+Y+0×(4-X-Y)=10.
∴Y=10-3X.
∴0≤X≤4.
∴当整数X=0,1,2,3,4时,Y=10,7,4,1,-2.
又∵0≤Y≤4且0≤X+Y≤4,
∴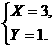
∴B队胜3场,平1场.
∵A队积9分,胜3场,
不妨设A队胜C、D、E队,负给B队.
又∵B队胜3场平1场,
∴不妨设B队又胜D、E队,于是C队平.
则这时已比赛7场,还有3场,即C--D,C--E,D--E,这3场比赛中无论哪个队,最多积分为6分小于A的积分.
∴A队一定出线且为第二名.
(4)如果小组中积分最高的队积9分,则这五个队中可能有M个队得9分.
∴20≤9M≤30,即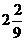 ≤M≤3
≤M≤3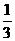 .
.
∴正整数M=3,
即有3个队都可能为9分,即都可能胜3场负1场.
由规则知,只取前两名且获胜场数相等时据进球分数排名,由此可知,A队不一定出线.
9.一个玩具厂用于生产的全部劳力最多为455个工时,原料最多为410个单位.生产一个小熊要使用15个工时,20个单位的原料,最高售价为80元;生产一个小猫要使用10个工时,5个单位的原料,最高售价45元,在劳力和原料的限制下合理地安排生产小熊、小猫的个数,可以使小熊、小猫的总售价尽可能高.请你用学过的数学知识分析,总售价是否可能达到2 200元?
解:假设能够达到2 200元,则有80×小熊?数+45×小猫数=2 200,又有15×小熊数+10×小猫数≤455,20×小熊数+5×小猫数≤410.
设生产小熊x个,生产小猫y个可以使总售价达2 200元.根据题意,得
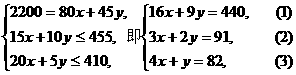
由①得y=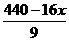 ,
④
,
④
把④代入②③,得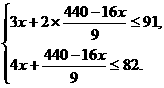
解这个不等式组得12.2≤x≤14.9,所以x=13,x=14.
当x=13时,y=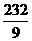 ;当x=14时,y=24.
;当x=14时,y=24.
所以安排生产小熊14个,小猫24个,可使总销售价达到2 200元.
8.(2010湖南益阳模拟,21(1))城西中学七年级学生共400人,学校决定组织该年级学生到某爱国主义教育基地接受教育,并安排10位教师同行.经学校与汽车出租公司协商,有两种型号的客车可供选择,其座位数(不含司机座位)与租金如下表,学校决定租用客车10辆.为保证每人都有座位,显然座位总数不能少于410.设租大巴x辆,根据要求,请你设计出可行的租车方案共有哪几种?
|
|
大巴 |
中巴 |
|
座位数(个/辆) |
45 |
30 |
|
租金(元/辆) |
800 |
500 |
解:根据不等关系,坐位总数大于等于410,租用客车最多为10辆,得
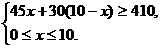
解得7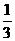 ≤x≤10.
≤x≤10.
又因为车辆数只能取整数,所以x=8,9,10.
租车方案共3种:租大巴8辆,中巴2辆;租大巴9辆,中巴1辆;租大巴10辆,不租中巴.
7.(2010湖北十堰模拟,22)市“康智”牛奶乳业有限公司经过市场调研,决定从明年起对甲、乙两种产品实行“限产压库”,要求这两种产品全年共新增产量20件,这20件的总产值P(万元)满足:110<P<120.已知有关数据如下表所示,那么该公司明年应怎样安排新增产品的产量?
|
产品 |
每件产品的产值 |
|
甲 |
4.5万元 |
|
乙 |
7.5万元 |
解:设该公司安排生产新增甲产品x件,那么生产新增乙产品(20-x)件,由P=甲产品的件数×4.5+乙产品的件数×7.5,代入110<P<120,
得110<4.5x+7.5(20-x)<120,
解这个不等式组,得10<x<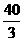 ,
,
依题意,得x=11,12,13.
当x=11时,20-11=9;当x=12时,20-12=8;当x=13时,20-13=7.
所以该公司明年可安排生产新增甲产品11件,乙产品9件;或生产新增甲产品12件,
乙产品8件;或生产新增甲产品13件,乙产品7件.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com