
题目列表(包括答案和解析)
1.某商店同时卖出两套服装,每套均卖168元,以成本算,其中一套盈利20%,另一套亏本20%,则这次出售中,商贩( )
A.不赚不赔 B.赚了37.3元 C.赚了14元 D.赔了14元
解析:设盈利的一套服装的进价为x元,亏本的一套服装的进价为y元,则由题意得x(1+20%)=168,y(1-20%)=168.解得x=140,y=210.这样成本为210+140=350(元),而售价为168+168=336(元),所以赔了14元.
答案:D
4.如图8-3-1,将正方形ABCD的一角折叠,折痕为AE,∠BAD比∠BAE大48°.设∠BAE与∠BAD的度数分别为x、y,则可得到方程组为________________.
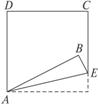
图8-3-1
解析:根据等量关系(1)∠BAD-∠BAE=48°,(2)∠BAD+2∠BAE=90°可列方程组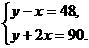
答案: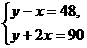
10分钟训练(强化类训练,可用于课中)
3.小明对小亮说:“我比你大8岁.”小亮却说:“我的年龄的两倍比你大3岁.”请你根据以上对话填空:小明今年___________岁,小亮今年_____________岁.
解析:此题需在对话中找到等量关系:小明的年龄=小亮的年龄+8;小亮的年龄×2-小明的年龄=3,所以只要设小明的年龄为x,小亮的年龄为y,就可列出方程组.
根据题意有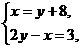
即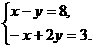 所以两式相加得y=11.则x=11+8=19.所以小明今年19岁,小亮今年11岁.
所以两式相加得y=11.则x=11+8=19.所以小明今年19岁,小亮今年11岁.
答案:19 11
2.买甲、乙两种纯净水共用250元,其中甲种水每桶8元,乙中水每桶6元,乙种水的桶数是甲种水的桶数的75%,设买甲种水x桶,乙种水y桶,则所列方程组正确的是( )
A.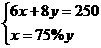 B.
B.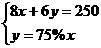
C.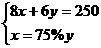 D.
D.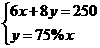
解析:根据等量关系(1)买甲种水的钱数+买乙种水的钱数=250,(2)乙桶的个数=甲种水的桶数的75%,可得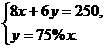
答案:B
1.八年级(3)班共有学生349人,其中男生人数y比女生人数x的2倍少4人,则下列方程组中正确的是( )
A.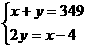 B.
B.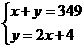
C.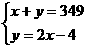 D.
D.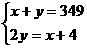
解析:审清题意后找出两个等量关系:男生人数y+女生人数x=349;男生人数y=女生人数x的2倍-4.所以由此列式得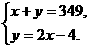
答案:C
8.3 再探实际问题与二元一次方程组
5分钟训练(预习类训练,可用于课前)
12.两根长度均为a cm的绳子,分别围成一个正方形和一个圆.
(1)如果要使正方形的面积不大于25 cm2,那么绳长a应满足怎样的关系式?
(2)如果要使圆的面积大于100 cm2,那么绳长a应满足怎样的关系式?
(3)当a=8时,正方形和圆的面积哪个大?a=12呢?
(4)你能得到什么猜想?改变a的取值再试一试.
解:这是一个等周问题,所围成的正方形面积可表示为(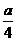 )2,圆的面积可表示为π(
)2,圆的面积可表示为π( )2.
)2.
(1)要使正方形的面积不大于25 cm2,就是(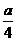 )2≤25,即
)2≤25,即 ≤25.
≤25.
(2)要使圆的面积大于100 cm2,就是π( )2>100,即
)2>100,即 >100.
>100.
(3)当a=8时,正方形的面积为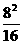 =4(cm2),圆的面积为
=4(cm2),圆的面积为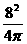 ≈5.1(cm2),4<5.1,此时圆的面积大;
≈5.1(cm2),4<5.1,此时圆的面积大;
当a=12时,正方形的面积为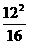 =9(cm2),圆的面积为
=9(cm2),圆的面积为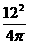 ≈11.5(cm2).
≈11.5(cm2).
9<11.5,此时还是圆的面积大.
(4)周长相同的正方形和圆,圆的面积大.本题中即 >
> .
.
11.小明和小亮决定把省下的零用钱存起来,已知小明存了168元,小亮存了85元,从这个月开始小明每月存16元,小亮每月存25元,几个月后小亮的存款数能超过小明?
解:设x个月后小亮的存款数能超过小明,则第x个月后小明的存款数为(16x+168)元,小亮的存款数是(25x+85)元.
所以由题意可得25x+85>16x+168,25x-16x>168-85,即9x>81,得x>9.
故9个月后小亮的存款数能超过小明.
10.某辆救护车向相距120千米的地震灾区运送药品需要1小时送到,前半小时已经走了50千米,后半小时至少以多大的速度前进,才能保证及时送到?
解:设后半小时速度为x千米/时,
依题意,有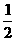 x+50≥120.
x+50≥120.
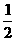 x≥70,x≥140.
x≥70,x≥140.
故后半小时至少以140千米/时的速度前进才能保证及时送到.
9.你能比较2 0052010与2 006的大小吗?
为了解决这个问题,我们可先探索形如:n(n+1)和(n+1)n的大小关系(n≥1,自然数).
为了探索其规律可从n=1、2、3、4?、…这些简单的情形入手,从中观察、比较、猜想、归纳并得出结论.
(1)利用计算器比较下列各组中两个数的大小:(填“<”“>”)
①12____________21;②23____________32;③34____________43;④45____________54;
⑤56____________65.
(2)试归纳出nn+1与(n+1)n的大小关系是:______________.
(3)运用归纳出的结论,试比较2 0052010与2 006的大小.
解:(1)通过计算可得< < > > >
(2)经过观察、比较、猜想可归纳出,
当n=1,2时,nn+1<(n+1)n;
当n>3时,nn+1>(n+1)n.
(3)根据规律,当n>3时,nn+1>(n+1)n,得
2 0052 006>2 0062 005.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com