6.下列说法错误的是(　 )

　　 A.同位角不一定相等　　　 B.内错角都相等

　　 C.同旁内角可能相等　　　 D.同旁内角互补,两直线平行

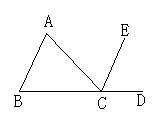
5.如图3所示,能判断AB∥CE的条件是(　 )

　　 A.∠A=∠ACE　　 B.∠A=∠ECD　　 C.∠B=∠BCA　 D.∠B=∠ACE

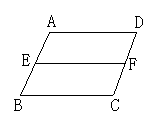
4.如图2所示,如果∠D=∠EFC,那么(　 )

A.AD∥BC　　 B.EF∥BC　　 C.AB∥DC　　 D.AD∥EF

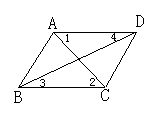
3.如图1所示,下列条件中,能判断AB∥CD的是(　 )毛

A.∠BAD=∠BCD　　　 B.∠1=∠2;　　 C.∠3=∠4　　　 D.∠BAC=∠ACD

　　　　 (1)　　　　　　　　　　 (2)　　　　　　　　　　 (3)

2、在同一平面内,两条不重合直线的位置关系可能是(　 )毛

A.平行或相交　　 B.垂直或相交　　 C.垂直或平行　　 D.平行、垂直或相交

1、下列说法正确的有(　 )

①不相交的两条直线是平行线;　 ②在同一平面内,不相交的两条线段平行

③过一点有且只有一条直线与已知直线平行;　 ④若a∥b,b∥c,则a与c不相交.

A.1个　　 B.2个　　 C.3个　　 D.4个

10.在日常生活中，观察各种建筑物的地板，就能发现地板常用各种正多边形地砖铺砌成美丽的图案.也就是说，使用给定的某些正多边形，能够拼成一个平面图形，既不留下一丝空白，又不互相重叠(在几何里叫做平面镶嵌)，这显然与正多边形的内角大小有关.当围绕一点拼在一起的几个多边形的内角加在一起恰好组成一个周角(360°)时，就拼成了一个平面图形.

(1)请根据下列图形，填写表中空格.

图7-4-10

(2)如果限于用一种正多边形镶嵌，哪几种正多边形能镶嵌成一个平面图形？

答：___________________________________________________.

(3)从正三角形、正四边形、正六边形中选一种，再在其他正多边形中选一种，请画出用这两种不同的正多边形镶嵌成的一个平面图形(草图)；并探索这两种正多边形共能镶嵌成几种不同的平面图形？说明你的理由.

解析：用不同的正多边形拼凑起来的地砖铺平面，就必须使在某一点处几块地砖的各角合起来构成360°.

(1)108°　 120°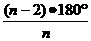　

(2)正三角形、正方形、正六边形

(3)解：如正方形和正八边形，草图如右图.

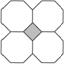
理由：设在一个顶点周围有m个正方形的角，n个正八边形的角，那么，m、n应是方程m·90°+n·135°=360°的整数解，即2m+3n=8的整数解.

又∵这个方程的整数解只有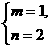一组，∴符合条件的图形只有一种.

9.如图7-4-9所示，用正五边形的地砖进行铺满平面是无法办到的，你能说出图中空隙是什么图形吗？它的每一个内角各是多少？

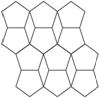
图7-4-9

解：由于正五边形的各边都相等，所以空隙处为菱形.

根据图形特点知：“菱形的一个锐角+3个正五边形的内角=360°.”

由于正五边形的每个内角为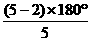=108°，所以菱形的锐角度数为360°-108°×3=36°.所以菱形的钝角的度数为180°-36°=144°.

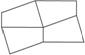
8.我们知道，任意四边形的内角和都等于360°，红光木器厂的工人师傅准备用一批形状、大小完全相同，但不规则的四边形边脚余料来铺设地板.你认为工人师傅这样做行吗？请你用一叠白纸剪一些这样的任意四边形拼一拼.(如图7-4-8)

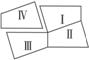
图7-4-8

解：当围绕一点拼在一起的几个多边形的内角加在一起恰好组成一个周角时，就拼成一个平面图形.因为四边形的内角和是360°，四块形状、大小完全相同，但不规则的四边形按下图就可以拼在一起.

下图是用任意的四边形材料拼成的地板示意图.

7.一个六边形的花坛周围用正三角形和正方形的砖块铺路，如图7-4-7，以正六边形花坛为中心向外共铺10层，则铺设整个路面共需要正三角形和正方形的砖块总数为多少？

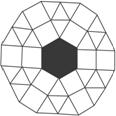
图7-4-7

解：图形铺满特点是，正方形铺在六边形的边上，其余的位置用三角形来铺.

由图形可知，正方形的砖块仅仅铺在六边形的各边的方向上，所以共需正方形砖块6×10=60块，从六边形的每个角铺去的都是三角形砖块，所以从每个角用去的三角形砖块有1+3+5+7+9+11+13+15+17+19=100块，所以共需三角形砖块600块.所以铺设整个路面共需要正三角形和正方形的砖块总数为660块.