课前热身

1.如果三角形的三个边长之比为3∶4∶5，且周长是24，则三边长分别为_____________.

答案：6、8、10

14.(2010河北)探索在如图7-23至图7-25中，△ABC的面积为a.

(1)如图7-23，延长△ABC的边BC到点D，使CD=BC，连接DA.若△ACD的面积为S₁，则S₁=__________(用含a的代数式表示)；

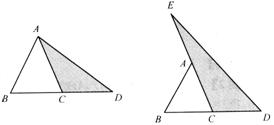
图7-23　　　　　　　　 图7-24

(2)如图7-24，延长△ABC的边BC到点D，延长边CA到点E，使CD=BC，AE=CA，连接DE.若△DEC的面积为S₂，则S₂=________(用含a的代数式表示)，并写出理由；

(3)在图7-25的基础上延长AB到点F，使BF=AB，连接FD，FE，得到△DEF(如图7-25).若阴影部分的面积为S₃,则S₃=__________(用含a的代数式表示).

图7-25

发现

　　 像上面那样，将△ABC各边均顺次延长一倍，连接所得端点，得到△DEF(如图7-25)，此时，我们称△ABC向外扩展了一次.可以发现，扩展一次后得到的△DEF的面积是原来△ABC面积的__________倍.

应用

　　 去年在面积为10 m²的△ABC空地上栽种了某种花卉.今年准备扩大种植规模，把△ABC向外进行两次扩展，第一次由△ABC扩展成△DEF，第二次由△DEF扩展成△MGH(如图7-26).求这两次扩展的区域(即阴影部分)面积共为多少平方米?

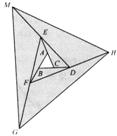
图7-26

答案：(1)a；(2)2a

理由：连接AD，∵CD=BC，AE=CA，

∴S_△DAC=S_△DAE=S_△ABC=a，

∴S₂=2a.

(3)6a　 7　 拓展区域的面积：(7²-1)×10=480(m²).

13.如图7-22，若AD是△ABC的角平分线，DE∥AB

(1)若DF∥AC，EF交AD于点O.试问：DO是否为△EDF的角平分线?并说明理由；

(2)若DO是△EDF的角平分线，试探索DF与AC的位置关系，并说明理由.

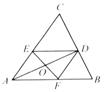
图7-22

答案：(1)DO是△DEF的角平分线，理由如下：由DE∥AB，得∠EDA=∠DAF.由DF∥AC，得∠EAD=∠ADF.

又AD是△ABC的角平分线，有∠EAD=∠DAF

所以∠BDA=∠ADF.(2)DF∥AC.理由略

12.(广西)图7-21是某广告公司为某种商品设计的商标图案，若图中每个小长方形的面积都是1，则阴影部分的面积是(　　 )

A.6　　　　　　　　 B.6.5　　　　　　　　　 C.7　　　　　　　　 D.7.5

答案：B(点拨：阴影部分面积=大长方形面积-空白部分面积和)

模拟在线

11.(陕西)如图7-20，在锐角△ABC中，CD、BE分别是AB、AC边上的高，且CD、BE交于一点P，若∠A=50°，则∠BPC的度数是(　　 )　

A.150°　　　　　　 B.130°　　　　　　　 C.120°　　　 　　　D.100°

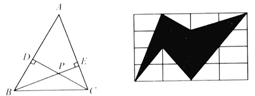
图7-20　　　　　　 图7-21

答案：B

10.如图7-19，在△ABC中，已知点D、E、F分别为BC、AD、CE的中点，且S_△ABC=4c m²，则S_阴影=__________.

图7-18　　　　　　　　 图7-19

答案：1 cm²

9.已知BD、CE是△ABC的高，直线BD、CE相交所成的角中有一个角是50°，则∠BAC等于__________.

答案：50°或130°

8.如图7-18，△ABC中，∠ACB=90°，把△ABC沿直线AC翻折180°，使B点落在B′点的位置，则线段AC是__________.

答案：△ABB′的中线、角平分线和高

7.如图7-17，BD是△ABC的中线，若AB=8 cm，AC=6 cm，BC=6cm　 则△ABD与△BCD的周长之差为__________.

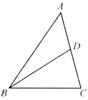
图7-17

答案：2 cm.

6.如图7-16，E、F分别是△ABC的边AC、AB的中点，FD⊥AC，则BE、CF分别是△ABC的边AC、AB上的_______；EF既是_______的中线，又是______的中线；FD是______的高.

答案：中线；△ABE；△ACF；△ACF(答案不唯一)

课下作业