2.等式两边都加上(或减去)＿＿＿＿或＿＿＿＿,所得结果仍是等式.思路解析：根据等式基本性质1.

答案：同一个数　同一个代数式

1.若方程3(x+4)－4=2k+1的解是－3，则k的值是(　)

A.1　　　B.－1　　　C.0　　　D.－

思路解析：既然x=－3是方程3(x+4)－4=2k+1的解，就说明－3可以代替x的位置，也就是把原题中的x换成“－3”，得3×(－3+4)－4=2k+1，可求得k=－1.

答案：B

12.(2010山东青岛模拟) 五一黄金周期间，某学校计划组织385名师生租车旅游，现知道出租公司有42座和60座两种客车，42座客车的租金每辆为320元，60座客车的租金每辆为460元．

(1)若学校单独租用这两种车辆各需多少钱？

(2)若学校同时租用这两种客车8辆(可以坐不满)，而且要比单独租用一种车辆节省租金．请你帮助该学校选择一种最节省的租车方案．

解析：本题与社会生活实际联系密切，综合性很强，要用到等式和不等式(组)来解决.关键是找出题目中的等量和不等量关系.

答案：(1)385÷42≈9.2，

∴单独租用42座客车需10辆，租金为320×10=3 200元．

385÷60≈6.4，

∴单独租用60座客车需7辆，租金为460×7=3 220元．

(2)设租用42座客车x辆，则60座客车(8-x)辆，由题意得：

解之得：．

∵x取整数，∴x可以取4或5．

当x=4时，租金为320×4+460×(8-4)=3 120元；

当x=5时，租金为320×5+460×(8-5)=2 980元．

答：租用42座客车5辆，60座客车3辆时，租金最少.

11.(2010甘肃张掖模拟) 为节约用电，某学校在本学期初制定了详细的用电计划．如果实际每天比计划多用2度电，那么本学期的用电量将会超过2 990度；如果实际每天比计划节约2度电，那么本学期的用电量将不超过2 600度．若本学期的在校时间按130天计算，那么学校原计划每天用电量应控制在什么范围内？

解析：根据“实际每天比计划多用2度电，那么本学期的用电量将会超过2 990度；如果实际每天比计划节约2度电，那么本学期的用电量将不超过2 600度”找出两个不等量关系；注意超过用“>”表示，不超过用“≤”表示.

答案：设学校原计划每天用电量为x度，依题意得

解得21＜x≤22．

即学校每天的用电量应控制在21-22度(不包括21度)范围内．

10.(2010福建南平模拟) 解不等式组

解析：先求出每个不等式的解集，再根据“大大取较大，小小取较小，大小小大中间找，大大小小解不了”确定不等式组的解集.

答案：由①得x-3x≤2，∴x≥-1，

由②得3(x-1)≤2x，∴3x-2x≤3，

∴x≤3，∴不等式组的解集为：-1≤x≤3.

9.广州“五军”足球队在已赛过的20场比赛中，输了30%，平局20%，该队还要赛若干场球，球迷发现，即使该队以后每场球都没有踢赢，它也能保持不低于30%胜场数，求该足球队参赛数最多有多少场？

解析：要注意弄清题中百分数的含义．

答案：设该足球队参赛数最多有x场，有：

≥30%·x，

x≤，

又x为整数，所以参赛场数最多有33场．

8.某工程，甲工程队单独做40天完成，若乙工程队单独做100天完成．将工程分两部分，甲做其中一部分用了x天，乙做另一部分用了y天，其中x、y均为正整数，且x<15，y<70，求x、y．

解析：根据题意知道，甲、乙完成的工作量之和应等于总的工作量(常设为1)，据此可以得到一个关于x、y的关系式，可以用其中的一个未知数把另一个未知数表示出来，然后代入到条件x<15，y<70中去，求出它们的范围，进一步结合x、y均为正整数可以求出它们的值．

答案：设甲做其中一部分用了x天，乙做另一部分用了y天，

所以=1，即y=100-x，又x<15，y<70，

所以

解之得：12<x<15，所以x=13或14，

又y也为正整数，所以x=14，y=65．

7.已知方程组：的解为正数，求a的取值范围．

解析：先求出方程组的解，把x-y分别用含有a的字母表示出来，然后根据x、y均为正数，建立不等式组，求出a的范围．

答案：解这个方程组得：

由题意有：

解得

所以-＜a＜4．

6.已知一个球队共打了14场比赛，其中赢的场数比平的场数和输的场数都要少，那么这个球队最多赢了_______场．

解析：设这个球队赢了x场，平了y场，输了z场，

由题意有：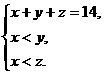

故x+x+x＜x+y+z,即3x<14,x＜，

又x为整数，故x最大为4．

答案：4

综合·应用

5.某射击队员在一次比赛中，前7次射击共中60环，而其余选手已全射完，最好成绩是87环，该队员要想夺冠，第8次射击至少为_______环．

解析：已进行了7次射击，还有3次，最后2次射击最多20环，故第八环必须大于87-60-20=7(环)，即第八次至少要射中8环．

答案：8