1.下面给出的四条线段中，最长的是( )

(A)a　 (B)b　　 (C)c　 (D)d

11.服装厂用355米布做成人服装和儿童服装,成人服装每套平均用布3.5米,儿童每套平均用布1.5米,现在已做了80套成人服装,用余下的布还可以做几套儿童服装?

思路解析：如果设余下的布可以做x套儿童服装,那么这x套儿童就需要布1.5x米,根据题意可以列方程:

解:设余下的布可以做x套儿童服装,那么这x套服装就需要1.5x米,根据题意,得

80×3.5+1.5x=355,

化简,得280+1.5x=355,

两边减280,得1.5x=75,

两边除以1.5,得x=50.

答：用余下的布还可以做50套儿童服装.

10.利用等式性质解方程：－x+3=－10.

思路解析：利用等式的性质先去分母,再化为x=a的形式.

答案：x=

9.已知5a－3b－1=5b－3a，利用等式的性质比较a、b的大小.

解:利用等式的性质将它们移到等式的同一侧，即5a+3a－1=5b+3b，再进行化简，得8a－1=8b，最后用作差法比较大小，即8a－8b=1，8(a－b)=1，a－b=＞0，所以a＞b.

8.下列方程中以x=为解的是(　)

A.－2x=4

B.－2x－1=－3

C.－x－1=－

D.－x+1=

思路解析：如果将四个选项中的方程一一求解，当然可以解决问题，但是这样做效率太低.根据方程的解的意义，可将代入四个选项中进行验证.只有D选项的方程左右两边的值是相等的.

答案：D

7.若－8x^3a+2＝1是一元一次方程，则a＝＿＿＿＿.

思路解析：因为一元一次方程中未知数的指数是1，所以－8x^3a+2中x的指数3a+2就是1.

解：由题意得

3a+2＝1，

3a+2－2＝1－2--等式基本性质1

3a＝－1，

=--等式基本性质2

a＝－.

答案:-

6.若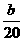－=-,则a=＿＿＿＿＿＿这是根据等式的性质,在等式两边同时＿＿＿＿＿＿.

思路解析：根据等式基本性质2.

答案：5b　乘以－100

综合·应用·创新

5.若－6a=4.5,则＿＿＿＿＿＿=－1.5,这是根据等式的性质,在等式两边同时＿＿＿＿＿＿.

思路解析：根据等式基本性质2.

答案：2a　除以－3

4.若2x－a=3,则2x=3+＿＿＿＿＿＿,这是根据等式的性质1,在等式两边同时＿＿＿＿＿＿.

思路解析：等式两边同时加上(或减去)同一个数,所得结果仍是等式.

答案：a　加上a

3.等式两边都乘以(或除以)＿＿＿＿(　　)，所得结果仍是等式.

思路解析：根据等式基本性质2.

答案：同一个数　除数不为0