
题目列表(包括答案和解析)
13.(2010福建晋江模拟) 正十二边形的每一个外角等于_________.
解析:由正多边形的定义可知正多边形的每一个外角都相等,多边形的外角和为固定值360°,所以正十二边形的每一个外角度数为:360°÷12=30°.
答案:30°
12.(2010广东佛山高中招生考试) 内角和与外角和相等的多边形一定是( )
A.八边形 B.六边形
C.五边形 D.四边形
解析:多边形的外角和为固定值360°,所求的多边形的内角和为360°,由多边形内角和公式:(n-2)×180°=360°可求得n=4.
答案:D
11.(2010北京丰台模拟) 七边形的内角和是( )
A.360° B.720° C.900° D.1 260°
解析:由多边形内角和公式,(7-2)×180°=900°.
答案:C
10.是否存在一个多边形,它的每个内角都等于相邻外角的 ?为什么?
?为什么?
解析:存在型问题的一般解决方法是,假设存在,经过合理的推理论证,如果得出矛盾(与定义、定理、公理或实际问题不符)说明假设不成立;如果与定义、定理、公理或实际问题相符,说明假设不成立,即存在.
答案:不存在,理由是:
如果存在这样的多边形,设它的一个外角为α,则对应的内角为180°-α,于是:
 ×α=180°-α,解得α=150°.
×α=180°-α,解得α=150°.
这个多边形的边数为:360°÷150°=2.4,而边数应是整数,因此不存在这样的多边形.
9.在四边形的四个内角中,最多能有几个钝角?最多能有几个锐角?
解析:从四边形内角和等于360°考虑.
答案:最多能有三个钝角,最多能有三个锐角.理由是:
设四边形的四个内角的度数分别为:α,β,γ,δ,则α+β+γ+δ=360°,α、β、γ、δ的值最多能有三个大于90°.
若α、β、γ、δ都大于90°,α+β+γ+δ>360°.
同理最多能有三个小于90°.
8.如图7-3-14,六边形ABCDEF的内角都相等,∠DAB=60°,AB与DE有什么关系?BC与EF有这种关系吗?这些结论是怎么得出的?

图7-3-14
解析:利用多边形内角和公式分别求出正六边形各内角及∠ADC的度数,进而求得∠ADE,然后用平行线的判定进行推断.
答案:依题意有正六边形内角= =120°,
=120°,
即∠B=∠C=∠E=∠F=∠BAF=∠CDE=120°.
所以在四边形ABCD中,∠ADC=360°-60°-∠B-∠C=60°.
所以∠ADE=120°-∠ADC=60°.所以∠ADE=∠DAB.所以DE∥AB.
BC与EF也互相平行,
因为∠DAB+∠B=60°+120°=180°,所以BC∥AD.
又因为∠E+∠ADE=120°+60°=180°,所以EF∥AD,所以BC∥EF.
7.看图答题:
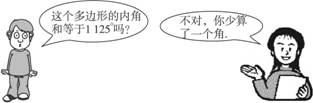
图7-3-13
问题:(1)小华在求几边形的内角和?
(2)少加的那个角为多少度?
解析:设小华求的多边形是n边形,则1 125°应大于(n-1)边形内角和,而小于n边形内角和,结合n为正整数可求出n的大小.
答案:(1)设多边形为n边形有:
(n-1-2)·180°<1 125°,解得n<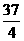 ,
,
(n-2)·180°>1 125°,解得n> ,
,
即n<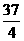 .且n>
.且n> ,又n为整数,所以n=9.
,又n为整数,所以n=9.
(2)n=9时,多边形内角和为(9-2)×180°=1 260°,少加的角度数为1 260°-1 125°=135°.
6.如图7-3-12所示,四边形ABCD中,∠B=∠D=90°,CF平分∠BCD.若AE∥CF,由公式判定AE是否平分∠BAD.说明理由.

图7-3-12
解析:结合四边形内角和与三角形内角和进行推理.
答案:AE平分∠BAD,理由如下:
因为AE∥CF,所以∠DEA=∠DCF,∠CFB=∠EAB,
又∠DCF=∠BCF,∠BCF+∠BFC=90°,∠DEA+∠DAE=90°,
所以∠DAE=∠BFC=∠EAB.
所以AE平分∠BAD.
综合·应用
5.一个五边形有三个内角是直角,另两个内角都等于n°,求n的值.
解析:直接根据多边形内角和公式求解.
答案:根据题意有:3×90+2n=(5-2)×180,得n=135.
4.如图7-3-11,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,∠A与∠1+∠2之间有一种数量关系保持不变,这个关系是( )
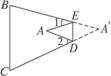
图7-3-11
A.∠A=∠1+∠2 B.2∠A=∠1+∠2
C.3∠A=2∠1+∠2 D.3∠A=2(∠1+∠2)
解析:根据题意有:∠A=∠A′,在△A′BC中,有∠B+∠C=180°-∠A′,在△ADE中,有∠ADE+∠AED=180°-∠A,又在四边形BCDE中有∠B+∠C+∠BED+∠CDE=360°,即∠B+∠C+∠1+∠AED+∠ADE+∠2=360°.所以有180°-∠A+∠1+∠2+180°-∠A=360°,故2∠A=∠1+∠2.
答案:B
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com