
题目列表(包括答案和解析)
1.________________的式子叫不等式.
5.1 不等式 同步练习
[主干知识]
认真预习教材,尝试完成下列各题:
9.1米长的小棒,第1次截去一半,第2次截去剩下的一半,如此截下去,第7次后剩下的小棒有多长?
思路解析:此题的关键是找出每次截完后,剩下的小棒占整根棒的比例与所截次数之间的关系.现将它们的关系列表如下:
|
所截次数 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
剩下] 木棒 比例 |
 |
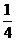 |
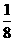 |
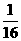 |
 |
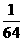 |
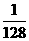 |
=( )1 )1 |
=( )2 )2 |
=( )3 )3 |
=( )4 )4 |
=( )5 )5 |
=( )6 )6 |
=( )7 )7 |
答案: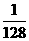 米.
米.
8.求(1-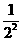 )×(1-
)×(1- )×(1-
)×(1-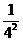 )…(1-
)…(1-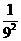 )×(1-
)×(1-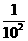 )的值.
)的值.
思路解析:由于每一项都可以 改写成两项积的形式,因此可利用分解相约的方法.
改写成两项积的形式,因此可利用分解相约的方法.
答案: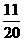 .
.
7.x2=64,x是几?x3=64,x是几?
思路解析:由于任何数的偶次幂都是正数或0,平方也是偶次幂,所以平方是64的数有可能是正数,也有可能是负数,这两个数互为相反数.先求出正数,再求出其相反数.
立方是正数(64)的数只能是 正数,因为负数的奇次幂为负数,所以立方是64的数只能有一个.
正数,因为负数的奇次幂为负数,所以立方是64的数只能有一个.
解:x=±8时,x2=64;x=4 时,x3=64.
时,x3=64.
6.若n为自然数,求(-1)2n-(-1)2n+1+( -2)3的值.
-2)3的值.
思路解析:因为n为自然数,所以2n为偶数,2n+1为奇数.由负数的奇次幂是负数,负数的偶次幂是正数可知: (-1)2n=1,(-1)2n+1=-1.
答案:-6.
5.已知a、b为有理数,且(a+ )2+(2b-4)2=0,求-a2+b2的值.
)2+(2b-4)2=0,求-a2+b2的值.
解:因为任意有理数的平方非负,可得:(a+ )2≥0,(2b-4)2≥0.又因为(a+
)2≥0,(2b-4)2≥0.又因为(a+ )2+(2b-4)2=0,得a+
)2+(2b-4)2=0,得a+ =0,a=-
=0,a=- ,2b-4=0,b=2,把a=-
,2b-4=0,b=2,把a=- ,
, b=2代入a2+b2,得3
b=2代入a2+b2,得3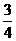 .
.
4.计算:
(1)-(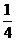 )2×(-4)2÷(-
)2×(-4)2÷(-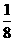 )2;
)2;
(2)(-33)×(-1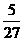 )÷(-42)×(-1)25.
)÷(-42)×(-1)25.
思路解析:本题是乘、除、乘方混合运算?运算时一要注意运算顺序:先乘方、后乘除,二要注意每一步运算中符号的确定.
解:(1)原式=-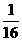 ×16÷
×16÷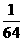 =-64;
=-64;
(2)原式=(-27)×(-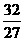 )÷(-16)×(-1)=27×
)÷(-16)×(-1)=27×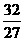 ×
×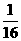 =2.
=2.
3.计算:
(1)(-5)4; (2)-54; (3)-(-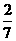 )3;
)3;
(4)[-(-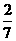 )]3; (5)-
)]3; (5)-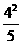 ; (6)(-
; (6)(-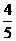 )2.
)2.
思路解析:本题意在考查对(-a)n与-an的意义的理解,要注意二者的区别与联系.
解:(1)原式=(-5)×(-5)×(-5)×(-5)=625;
(2)原式=-5×5×5×5=-625;
(3)原式=-(-
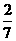 )(-
)(-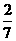 )(-
)(-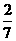 )=
)=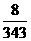 ;
;
(4)原式=(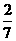 )3=
)3=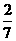 ×
×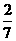 ×
×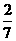 =
=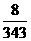 ;
;
(5)原式 =-
=-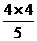 =-
=-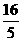 ;
;
(6)原式=(-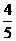 )(-
)(-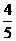 )=
)=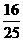 .
.
2.填空:
(1)若x<0且x2=49,则x=_______;
(2)若|x+2|+(y+1)2=0,则x=______,y=______,x3y2 002=_______;
(3)平方小于10的整数有_______个,其和为_______,积为________.
答案:(1)-7 (2)-2 -1 -8 (3)7 0 0
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com