
题目列表(包括答案和解析)
2.某小店一周的收支情况如下(收入为正,支出为负,单位:元):
+141.8,-27.64,-5,+84,-16.8,-31.09,+125.7.
收支相抵后,合计收入(或支出)多少元?
思路解析:根据题意都可转化为有理数的加法来解决.
解:(+141.28)+(-27.64)+(-5)+(+84)+(-16.8)+(-31.09)+(+125.7)=270.45(元)
1.判断:
(1)(-4)+(-5)=-9;
(2)5+(-6)=-11;
(3)(-7)+10=3;
(4)(-2)+(+2)=4;
(5)两个数的和一定大于每一个加数;
(6)互为相反数的两个数的和等于0;
(7)若两个数的和为正数,则这两个数都是正数.
思路解析:对于判断题要全面分析,特别是从反面去思考,能不能举出反例.
答案:(1)√ (2)× (3)√ (4)× (5)× (6)√ (7)×
9.有一种“算24 ”的游戏,其规则是:任取四个1-13之间的自然数,将这四个数(每数只能用一次)进行
”的游戏,其规则是:任取四个1-13之间的自然数,将这四个数(每数只能用一次)进行 加减乘除混合运算,其结果为24.例如2,3,4,5作运算.(5+3-2)×4=24,现有四个有理数3、4、-6、10,运用以上规则写出等于24的算式,你能写出几种算法?
加减乘除混合运算,其结果为24.例如2,3,4,5作运算.(5+3-2)×4=24,现有四个有理数3、4、-6、10,运用以上规则写出等于24的算式,你能写出几种算法?
答案:例如:3×(10+4-6)=24.其他略.
8.计算:(-191 919×9 898+989 898×1 919)÷(-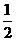 +3.14).
+3.14).
思路解析:此题看上去好像计算量很大,但仔细观察分子可发现,19 1919=19×10 101,9 898=98×101,989 898=98×10 101,1 919=19×101,这样一来,两个积互为相反数,相加得0.
答案:0
7.计算:(-317÷158+1÷365×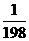 )×(2
)×(2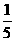 +1-
+1-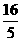 ).
).
思路解析:前一个括号计算复杂,后一个括号则很特殊且简单,结果为零,因此有时不能只顾算前面忽视后面.
答案:原式=(-317÷158+1÷365×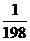 )×0=0.
)×0=0.
6.已知m除以5余1,n除以5余4,如果3m>n,求3m-n除以5的余数.
思路解析:此题应用了化除为乘的思想.
答案:3m-n除以5的余数是4.
5.混合运算:
(1) 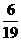 ÷(-1
÷(-1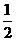 )×
)×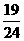 ; (2)(-81)÷2
; (2)(-81)÷2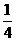 ×
×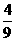 ×(-16);
×(-16);
(3)(-2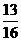 )÷(
)÷(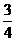 ×
×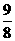 ); (4)|-1.3|+0÷(5.7×|-
); (4)|-1.3|+0÷(5.7×|-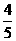 |+
|+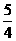 ).
).
思路解析:第(1)(2)小题应先把带分数化为假分数,然后进行运算;第(3)小题有括号,应先算括号里面的,再把除法转化为乘法进行计算;第(4)小题有0作被除数,早发现可使运算简便.
解:(1)原式=-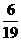 ×
×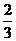 ×
×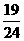 =-
=-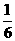 ;
;
(2)原式=81×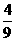 ×
×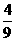 ×16=256;
×16=256;
(3)原式=-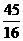 ×
×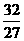 =-3
=-3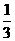 ;
;
(4)原式=1.3+0=1.3.
4.计算:
(1)29÷3×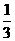 ;
;
(2)(-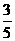 )×(-3
)×(-3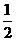 )÷(-1
)÷(-1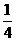 )÷3;
)÷3;
(3)[(+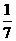 )-(-
)-(-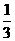 )-(+
)-(+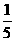 )]÷(-
)]÷(-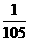 ).
).
思路解析:对于乘除混合运算,首先由负数的个 数确定符号,同时将小数化成分数,带分数化成假分数,算式化成连乘积的形式,再进行约分.(1)题注意乘除是同一级运算,应从左往右顺序运算,不能先做乘再做除;(3)题将除转化为乘的同时,化简中括号内的符号,然后用乘法分配律进行运算较简单.
数确定符号,同时将小数化成分数,带分数化成假分数,算式化成连乘积的形式,再进行约分.(1)题注意乘除是同一级运算,应从左往右顺序运算,不能先做乘再做除;(3)题将除转化为乘的同时,化简中括号内的符号,然后用乘法分配律进行运算较简单.
解:(1)原式=29×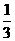 ×
×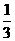 =
=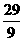 ;
;
(2)原 式=
式=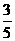 ×
×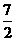 ×(-
×(-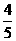 )×
)×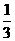 =-
=-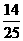 ;
;
(3)原式=(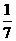 +
+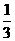 -
-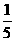 )×(-105)=-
)×(-105)=-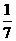 ×105-
×105-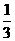 ×105+
×105+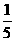 ×105=-15-35+21=-29.
×105=-15-35+21=-29.
3.计 算:(-
算:(-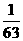 )÷(
)÷(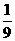 -
-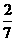 +
+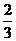 -
-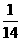 ).
).
思路解析:乘法对加法满足分配律,但除法对加法并不满足分配律.只有当把除法转化为乘法以后,才能运用分配律.
解:原式=-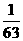 ÷(
÷(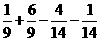 )=-
)=-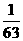 ÷
÷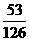 =-
=-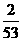 .
.
2.计算:
(1)(-1)÷(-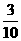 );
(2)(-0.33)÷(+
);
(2)(-0.33)÷(+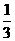 )÷(-9);[(3)(-9.18)×(0.28)÷(-10.71); (
)÷(-9);[(3)(-9.18)×(0.28)÷(-10.71); ( 4)63×(-1
4)63×(-1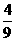 )+(-
)+(-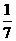 )÷(-0.9).
)÷(-0.9).
思路解析:先确定结果的符号,然后将除法运算转化成乘法运算.
解:(1)原式= ;
;
(2)原式=0.33×3×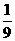 =0.11;
=0.11;
(3)原式=-9.18×0.28×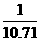 =-
=-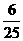 ;
;
(4)原式=63× (-1
(-1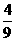 )+
)+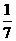 ×
×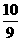 =-91+
=-91+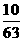 =-90
=-90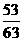 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com