1.一个有理数和它的相反数的乘积(　)

A.必定为正数　　 B.必定为负数

C.一定不大于0　　D.一定不小于0

思路解析：任意一个有理数，可能是正数、负数或0.

答案：C

3.求下列各数的相反数、倒数与绝对值：

+2.5，-3 ，1，0，|-5|，a，-b

思路解析：由定义求得.

2.比较大小：－_______-.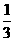

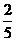思路解析：比较大小可以用数轴、绝对值，也可以用减法.根据“大－小＞0，小－大＜0”，用这两个数相减，若差大于0，第一个数大；若差小于0，第二个数大.

答案：＞

1.填空：

(1)(_____)+(－7)＝21;(2)(______)+(－27)＝－30;(3)(______)－12＝－17.

思路解析：第(1)(2)小题，已知和与其中一个加数，则另一个加数＝和－加数，“用减法”.而第(3)小题已知减数和差，求被减数，则被减数＝差+减数，“用加法”.

答案：(1) 28　 (2)－3　 (3)－5

5.矿井下A、B、C三处的标高分别是A(-37.5 m)、B(-129.7 m)、C(-73.2 m)，哪处最高？哪处最低？最高处与最低处相差多少？

思路解析：比较A、B、C三处的高低，就是比较这三个负数的大小，并求出最大数与最小数的差.

解：矿井下A处最高，B处最低，A处与B处相差92.2 m.

快乐时光

谁创造万物

某宗教学校的教师在课堂上厉声问学生：“你们说，是谁创造了世间万物？”

教室里鸦雀无声，大家屏住呼吸，不敢出大气.

教师许久听不到回答，更加火冒三丈地说：“我非要你们说不可！谁？”

说着，灯泡似的眼睛盯着一位学生.那位学生抖瑟瑟地站起来，说：“老师，不是我！”

30分钟训练(巩固类训练，可用于课后)

(4)(－3)－(－2)－(－1)－(+1.75).

思路解析：本题是有理数的减法运算，根据有理数减法法则，把减法全部转化为加法再进行计算，同时也可运用加法运算律使计算简便.

解：(1)原式=-1.5-3.6-4.3-5.2+9.4=-5.2；

(2)原式=- - + + =- + =- ；

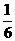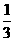(3)原式=2.75+4-0.71=6.04；

(4)原式=-3 +1 +2 -1 =-2+1=-1.

4.某地一年中最高气温35 ℃，最低气温－15 ℃，此地这一年的温差是多少？

解：温差＝最高温度－最低温度.这里的“－”是运算符号，不是减数的符号，所以当减数--最低温度不管是正数还是负数都要当作减数计算，与公式中的“－”要区别开.

3.计算：

(1)(-1.5)-(-9.4)-(+3.6)+(-4.3)-(+5.2)；

(2)0-(+)-(-)-(-)-(+)；

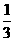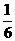2.计算：

(1)7.21-(-9.35);　　　　　　　 (2)(-19)-(+9.5)；

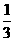(3)(+5 )-(+7 );　　 (4)(-4 )-(-4 )；

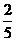(5)(-6.79)-(-6.79);　　 (6)(-3 )-(+3).

思路解析：按减法法则，把减法转化为加法计算.

答案：(1) 16.56　 (2) -28.5　 (3)-2 　(4) 　　(5)0　 (6)-7

1.判断题：

(1)两个数相减，就是把绝对值相减;　　　　　　　　　　　　　　　　　　　　　 (　　 )

(2)若两数的差为0，则这两数必相等;　　　　　　　　　　　　　　　　　　　　 (　　 )

(3)两数的差一定小于被减数;　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

(4)两个负数之差一定是负数;　　　　 　　　　　　　　　　　　　　　　　　　　(　　 )

(5)两个数的和一定大于这两个数的差;　　　　　　　　　　　　　　　　　　　 (　　 )

(6)任意不同号的两个数的和一定小于它们的差的绝对值.　　　　　　　　　　　　 (　　 )

思路解析：按减法法则和加法法则判断.

答案：(1)×　 (2)√　 (3)×　 (4)×　 (5)×　 (6)√

3.(1)某冷库温度是零下10 ℃，下降-3 ℃后又下降5 ℃，两次变化后冷库温度是多少？

(2)零下12 ℃比零上12 ℃低多少？

(3)数轴上A、B两点表示的有理数分别是-6 和7，求A、B两点的距离.

解：(1)(-10)-(-3)-(+5)=(-10)+(+3)+(-5)=(-15)+(+3)=-12.

(2)(-12)-(+12)=(-12)+(-12)=-24.

(3)|7 -(-6 )|=|7 +6 |=14 .

10分钟训练(强化类训练，可用于课中)