1.4.1　 有理数的乘法

5分钟训练(预习类训练，可用于课前)

1.4　 有理数的乘除法

9.若c，d互为倒数，则＝＿＿＿＿.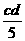

思路解析：互为倒数的两个数乘积为1.所以cd＝1.代入式子即可.

解：cd＝1，所以＝.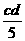

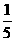答案：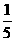

8.若ab＞0，且a+b＜0，则a＿＿＿＿0，b＿＿＿＿0.

思路解析：由ab＞0知，a与b是同号的(两数相乘，同号为正)，则a与b可能同时为正数，也可能同时为负数.又由a+b＜0知，若a与b同时为正数，和不会是负数，所以只能是“同时为负”这种情况了.

答案：＜　＜

7.a,b是什么有理数时,下式成立:

a×b=|a×b|.

思路解析： 当a,b两数其中至少有一个数为零时,该式一定成立,当a,b两数均不为零时,要注意等式右边是绝对值,是大于零的数,而a,b如果同号,也能保证a×b的积是正数.

答案：分3种情况

(1)当a>0,b>0时,等式a×b=|a×b|成立;

(2) 当a<0,b<0时,等式a×b=|a×b|成立;

(3)当a,b两数中至少有一个数为零时,等式a×b=|a×b|成立.

综合·应用·创新

6.如果abc＝0，那么一定有(　)

A.a＝b＝0B.a＝0，b≠0，c≠0

C.a、b、c至少有一个为0D.a、b、c最多有一个为0

思路解析：三个数乘积为0，说明因数中有零.但不能确定零的个数，也不能确定哪一个因数为零，所以只能选C.

答案：C

5.计算：

(1)(－125)×(－2)×(－8);

(2)(－7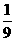)×(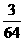－)×(－1);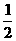

(3)22×(－33)×(－4)×0;

(4)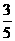－×(－2)×(－15).

解：(1)原式=－(125×2×8)=－2 000.

(2)原式=－(××)=－.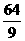

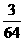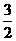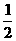(3)原式=0.

(4)原式=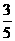－(×2×15)=－18.

4.如果两个有理数的积小于0，和大于0，那么这两个有理数(　)

A.符号相反

B.符号相反且绝对值相等

C.符号相反且负数的绝对值大

D.符号相反且正数的绝对值大

思路解析：两个数的积小于0，说明这两个数异号，和大于0，说明正数的绝对值大.

答案：D

3.两个有理数的积是负数，和为零，那么这两个有理数(　)

A.一个为0，另一个为正数　　B.一个为正数，一个为负数

C.一个为0，另一个为负数　　D.互为相反数且不等于0

思路解析：互为相反数的积为负，和为0.

答案：D

2.有两个有理数，它们的和为正数，它们的积也为正数，那么这两个有理数(　)

A.都是正数　　B.都是负数

C.一正一负　　D.符号不能确定

思路解析：运用两个有理数的加法法则与两个有理数的乘法法则进行判断.答案：A