
题目列表(包括答案和解析)
4.某单位买了35张戏票共用250元,其中甲种票每张8元,乙种票每张6元,则购买甲种票__________张,乙种票__________张.
答案:20;15
3.甲、乙二人按2∶5的比例投资开了一家公司,约定除去各项支出外,所得利润按投资比例分成,若第一年赢利14000元,那么甲、乙分别分得__________.
答案:4000元, 10000元
2.某铁路桥长为y m,一列长为x m的火车以上桥到过完桥共用30s,而整列火车在桥上的时间为20 s,若火车的速度为20m/s,则可列方程组为__________.
答案: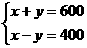
课上作业
课前热身
1.6年前,甲的年龄是乙的3倍,现在甲的年龄是乙的2倍,则甲现在的年龄是__________,乙现在的年龄是__________.
答案:24岁;12岁
14.(乌鲁木齐)为满足市民对素质教育的需求,某中学决定改变办学条件计划拆除一部分旧校舍、建造新校舍.拆除旧校舍每平方米需80元,建造新校舍每平方米需700元.计划在年内拆除旧校舍与建造新校舍共7200 m2,在实施中为扩大绿化面积,新建校舍只完成了计划的80%,而拆除校舍则超过了10%,结果恰好完成了原计划的拆、建的总面积.
(1)求原计划拆建面积各多少平方米?
(2)若绿化1 m2需200元,那么在实际完成的拆、建工程中节余的资金用来绿化大约是多少平方米?
答案:设拆旧校舍x m2, 建新校舍y m2,
则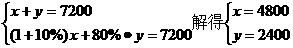
(2)节约资金:(4800×80-2400×700)-[4800×(1-10%)×80+2400×80%×700]=297600(元),用此资金可绿化面积是:297600÷200=1488(m2).即建新校舍2400m2.拆早校舍4800m2,实际用节约的资金用来绿化大约是1488m2.
作业30 §8.3 再探究实际问题与二元一次方程组(二)
典型例题
[例1] 如图8-5所示,长方形ABCD中,AB=8cm,BC=6 cm,且△BEC的面积比△DEF的面积大5 cm2,求DF的长.
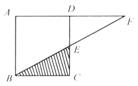
图8-5
[解析] 本题是数形结合题,未知数只有1个,若直接设DF的长为x cm,不易找到等量关系.可以分步来解,如没△BEC的面积为x cm2,△DEF的面积为y cm2,梯形ABED的面积为z cm2,求出△ABF的面积的y+2,再求DF就容易了.
[答案] 设△BEC的面积是x cm2,△DEF的面积是y cm2,四边形ABED的面积足2 cm2,则有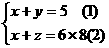
②-①,得y+z=43,即△ABF的面积为43 cm2.
设DF的长为acm,则有S△ABF=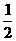 AB×(AD+DF),
AB×(AD+DF),
即43=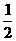 ×8×(6+a),所以a=
×8×(6+a),所以a=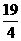 .
.
答:DF的长为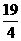 cm.
cm.
[例2] 一批货物要运往A地,货主准备租用汽车运输公司的甲、乙两种货车,乙知过去两次租用这两种货车的情况好下表:
|
|
第一次 |
第二次 |
|
甲种货车辆数(单位:辆) |
2 |
3 |
|
乙种货车辆数(单位:辆) |
3 |
6 |
|
累计运货吨数(单位:t) |
15.5 |
27 |
现租用该公司4辆甲种货车和1辆乙种货车,一次刚好运完这批货,如果按每吨付运费30元计算,问货主携带1000元是否够用?(不考虑其他费用)
[解析] 由表格中的信息求出甲、乙两种货车每次运货的吨数,再求出这批货物总吨数,算出需要的总费用,最后比较大小.
[答案] 设甲种货车每次运货x t,乙种货车每次运货y t,则有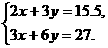
解得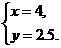
因此这批货物的总吨数为:4x+8y=4×4+8×2.5=36(t)
总费用为30×36=1080(元)
因为1080>1000,所以货主携带的钱不够用.
[例3] 有三块牧场,牧场里的草长得同样的密,同样的快,面积分别为3公顷、9公顷和21公顷;第一块牧场可借12头牛吃4个星期,第二块牧场可供20头牛吃9个星期,问第三块牧场可供多少头牛吃18个星期?
[解析] 本题等量关系不很明显,所以我们要充分挖掘和分析题目,确定以草量为等量关系列方程组.要知道可供多少头牛吃18个早期,要弄清草量由两部分组成的:一是原有草量,二是每周生出草量,显然每头牛每周吃的草量都是定值.关键是要找出这种供(原有草量和生长草量)与销(牛的吃草量)的关系.我们可用设而不求的方法解题.
[答案] 设每公顷原有草x t,每公顷每周生出新草y t,每头牛每周吃草a t,则有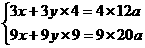 整理,得
整理,得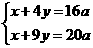 解得
解得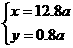
所以第三块牧场18个星期的总草量,可供牛吃6头数为:
 ≈31.7≈31
≈31.7≈31
答:第三块牧场可供31头牛吃18个星期.
总分100分 时间60分钟 成绩评定__________
13.(潍坊)甲、乙两件服装的成本共500元,商店老板为获取利润,决定将甲服装按50%的利润定价,乙服装按40%的利润定价,在实际出售时,应顾客要求,两件服装均按9折出售,这样商店共获利157元,求甲、乙两件服装的成本各是多少元?
答案:300元,200元
12.(2010河北)《九章算术》是我国东汉初年编订的一部数学经曲著作.在它的“方程”一章里,一次方程组是由算筹布置而成的.《九章算术》中的算筹图是竖排的,为看图方便,我们把它改为横排,如图8-3、图8-4.图中各行从左到右列出的算筹数分别表示未知数x,y的系数与相应的常数项.把图8-3所示的算筹图用我们现在所熟悉的方程组形式表达出来,就是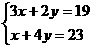 类似地,图8-4所示的算筹图我们可以表述为( )
类似地,图8-4所示的算筹图我们可以表述为( )

图8-3图 8-4
A.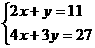 B.
B.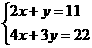
C.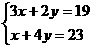 D.
D.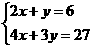
答案:A
模拟在线
11.某单位购买甲、乙两种纯净水共用250元,其中甲种水每桶8元,乙种水每桶6元;乙种水的桶数是甲种水桶数的75%.设买甲种水x桶,买乙种水y桶,则所列方程组中正确的是( )
A.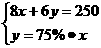 B.
B.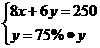
C.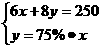 D.
D.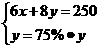
答案:C
10.在足球甲级A组的前11轮(场)比赛中,万达队连续不败,共积23分,按比赛规则,胜一场得3分,平一场得1分,那么该队胜与平的场次之比为___________.
答案:6∶5
9.通讯员从距1880m的总部骑马到前线,其中有一段泥泞路.已知马在干爽的道路上奔跑的速度为12km/h,在泥泞的道路上的平均速度为4.8 km/h,若通讯员从总部到前线共用16min,则他在干爽的道路上骑马的时间为___________.
答案:5min
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com