
题目列表(包括答案和解析)
5.如图7-1-24所示,A、B、C、D四点可以构成多少个三角形?请写出上述三角形.
解析:三角形是指由不在同一直线上的三条线段首尾顺次相接所组成的图形.
答案:可以构成4个三角形,它们是△ABC、△ABD、△ACD、△BCD.
4.如图7-1-23,△ABC中,AB⊥BC,AE、AD分别是△ABC的角平分线和中线,则BC边
上的高是_________,∠BAE_________=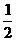 _________, BD_________=_________
_________, BD_________=_________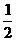 .
.
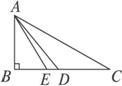
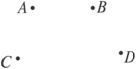
图7-1-23 图7-1-24
解析:根据定义作答.
答案:AB ∠CAE ∠BAC CD BC
3.图7-1-22中,BD=DE=EF=FC,那么___________是△ABE的中线.
A.AD B.AE
C.AF D.以上都是
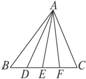
图7-1-22
解析:三角形的中线是指连结顶点和对边中点的线段,在△ABE中,BE的中线是AD.
答案:A
2.如图7-1-21,在△ABF中,∠B的对边是( )
A.AD B.AE C.AF D.AC
解析:在三角形中一个角的对边是以另外两个顶点为端点的边.[答案:C
1.如图7-1-20,以AB为边的三角形共有________个.
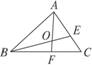
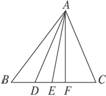
图7-1-20 图7-1-21
解析:以AB为边的三角形有△ABO、△ABE、△ABF、△ABC.
答案:4
12.(2010广东高中阶段学校招生考试) 如图7-2-27,已知:点B、F、C、D在同一直线上, AB∥ED,AC∥FE.请你根据上述条件,判断∠A与∠E的大小关系,并给出证明.
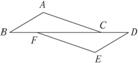
图7-2-27
解析:利用平行线的性质和三角形内角和定理完成证明.
答案:根据给定的条件,可得:∠A=∠E.
证明:∵AB∥ED,∴∠B=∠D.∵AC∥EF,∴∠1=∠2.
∵∠B+∠2+∠A=∠D+∠E+∠1=180°,∴∠A=∠E.
11.(湖北荆州模拟) 一副三角板,如图7-2-26所示叠放在一起.则图中∠α的度数是( )
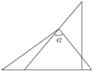
图7-2-26
A.75° B.60° C. 65° D.55°
解析:∠α与45°和60°这两个角构成一个三角形,因此由三角形的内角和等于180°,可求出∠α的度数应等于75°.
答案:A
10.以下列各组线段为边,能组成三角形的是( )
A.1 cm,2 cm,4 cm
B.8 cm,6 cm,4 cm
C.12 cm,5 cm,6 cm
C.2 cm,3 cm,5 cm
解析:能组成三角形的条件是:两边之和大于第三边.
答案:B
9.如图7-2-25,已知△ABC中,∠C=∠ABC=2∠A,BD是AC边上的高.求∠DBC的度数.
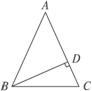
图7-2-25
解析:∠DBC在△BDC中,∠BDC=90°,为求∠DBC,应先求出∠C.
答案:设∠A=x°,则∠C=∠ABC=2x°,
∴x+2x+2x=180.
解得:x=36.
∴∠C=72°.
在△BDC中,∵∠BDC=90°,
∴∠DBC=180°-90°-72°.
∴∠DBC=18°.
8.如图7-2-24,已知BD、CD分别为△ABC外角∠EBC、∠FCB的角平分线,BD、CD相交于点D.小明看了后说,∠D=90°-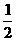 ∠A,小明说的对吗?为什么?
∠A,小明说的对吗?为什么?
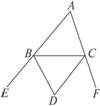
图7-2-24
解析:结合三角形内角和定理和三角形外角性质,找到∠B与∠A的关系.
答案:小明说的对.
因为∠EBC=∠A+∠ACB,∠FCB=∠A+∠ABC,
所以∠ABE+∠FCB=∠A+∠ACB+∠ABC+∠A=180°+∠A.
又∠DBC=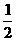 ∠EBC,∠BCD=
∠EBC,∠BCD=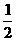 ∠BCF,
∠BCF,
∠BDC+∠BCD+∠D=180°,
所以∠D=180°-(∠BCD+∠DBC)
=180°-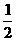 (∠EBC+∠FCB)
(∠EBC+∠FCB)
=180°-90°-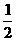 ∠A
∠A
=90°-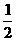 ∠A.
∠A.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com