4.a、b在数轴上的位置如图9-1-5，设M=a+b,N=-a+b,H=a-b, G=-a-b，则下列各式中正确的是(　　 )

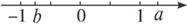
图9-1-5

A．M>N>H>G　　　　　　　　　　 B．H>M>G>N

C．H>M>N>G　　　　　　　　　　 D．G>H>M>N

解析：由于-1<b<0,a>1,所以a+b>0，-a+b<-1,-a-b<0,a-b>1.由于b＞0,H＞M,G＞N，故a-b>a+b>-a-b>-a+b．

答案：B

3.若x>y，则x-2________y-2；若x<y，a<0，则ax________ay．

解析：x>y，由不等式性质1有x-2>y-2,若x<y,a<0,由不等式性质3有ax>ay．

答案： >　 >

2.利用不等式的性质，填”>”或“<”

(1)若a>b,则2a+1________2b+1;

(2)若-1.25y<10,则y________-8;

(3)若a<b,且c>0,则ac+c________bc+c;

(4)若a>0,b<0,c<0,则(a-b)c________0.

解析：利用不等式的性质进行变形是不等式基本的变形，使用时特别要注意不等式性质3，即在不等式两边乘以(或除以)同一个负数时，不等号的方向要改变.

答案：(1)>　 (2)>　 (3)　 <　 (4)<

1.如图9-1-4,表示的是不等式的解集,其中错误的是(　　 )

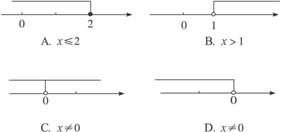
图9-1-4

解析：用数轴表示不等式的解集时要弄清两点：①包含这个点就用实心点，否则用空心点，②大于向右走,小于向左走.其中选项D表示的是x<0,而x≠0包括x>0和x<0两种情况.

答案：D

11.(重庆模拟) 如图7-1-26，在图1中，互不重叠的三角形共有4个，在图2中，互不重叠的三角形共有7个，在图3中，互不重叠的三角形共有10个…，则在第n个图形中，互不重叠的三角形共有_______个(用含n的代数式表示).

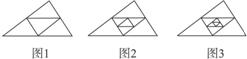
图7-1-26

解析：本题属于探索规律题目，解答此类题目一般解法是从特殊到一般，即从特殊例子入手猜想结论，然后进行验证.

答案：3n+1

10.(2010江苏盐城模拟) 已知三角形的三边长分别为4、5、x，则x不可能是(　　 )

A．3　　　　　 B．5 　　　　　　C．7　　　　　 D．9

解析：利用三角形三边关系解决.x的取值范围是：1＜x＜9.

答案：D

9.两根木棒的长分别是7 cm和10 cm,要选择第三根木棒，将它们钉成一个三角形，第三根木棒的长度有什么限制？

解析：根据三角形的三边关系：两边之和大于第三边，两边之差小于第三边，可选第三根木棒为第三边，它应该在两根木棒的差和两根木棒的和之间.这样列不等式即可求出.

答案：设第三根木棒的长为a cm，则根据三角形三边关系，可得

10-7＜a＜10+7.

所以3＜a＜17,

即第三根木棒应在3和17之间.

8.一个等腰三角形的周长为32 cm，腰长的3倍比底边长的2倍多6 cm.求各边长.

解析：像这样一类几何题，常常利用代数列方程的方法来解答.

答案：设底边长为x cm，则腰长为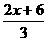，根据题意，可得：x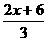+2×=32.

解得x =12.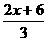=10.

答：这个三角形的三边长分别为10 cm、10 cm、12 cm.

7.如图7-1-25，△ABC中，D是BC边的中点，S_△ACD=12，求S_△ABC．

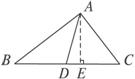图7-1-25

解析：过A作BC边的高AE，则S_△ABC=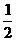BC·AE，S_△ACD=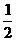CD·AE，结合中线找出S_△ABC和S_△ACD的关系．

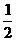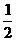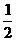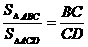答案：作AE⊥BC，且S_△ABC=BC·AE，S_△ACD=CD·AE，又D为AB的中点，所以CD=BC，所以=2．

所以S_△ABC=2S_△ACD=24．

6.已知三角形三边长分别为2、x、9，若x为奇数，则此三角形的周长为____________.

解析：利用三角形三边关系找到x的取值范围，由x为奇数确定x=9，从而求出三角形的周长.

答案：20

综合·应用