
题目列表(包括答案和解析)
4.已知8x+1<-2x,则下列各式中正确的是( )
A.10x+1>0 B.10x+1<0 C.8x-1>2x D.10x>-1
3.由x<y得ax>ay的条件是( )
A.a>0 B.a<0 C.a=0 D.无法确定
2.若a>b,则a-b>0,其根据是( )
A.不等式性质1 B.不等式性质2 C.不等式性质3 D.以上答案均不对
1.若x>y,用“>”或“<”填空:
(1)x-3_____y-3 (2)-3x______-3y
(3)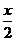 _______
_______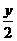 (4)-
(4)-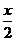 _______-
_______-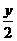
3.用a>b,用“>”或“<”填空.
(1)a+3______b+3 (2)a-5_____b-5 (3)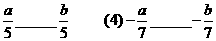
(5)3-a______3-b (6)-18-a_____-18-b
[典例分析]
例1 已知a<b,则下列四个不等式中不正确的是( )
A.4a<4b B.-4a<-4b C.a+4<b+4 D.a-4<b-4
思路分析:依据不等式的性质1,可得a+4<b+4,a-4<b-4,故C、D正确;依据不等式性质2,由a<b,可知4a<4b,故A正确;依据不等式性质3,由a<b,得-4a<-4b,故B不正确,应选B.
答案:B
方法点拨:本例重在考查不等式的三条基本性质,特别是性质3,两边同乘以(或除以)同一个负数时,一定要改变不等号的方向!这条性质是初学者最易出错也经常出错的地方.
例2 若a>0,b<0,c<0,则下列各式中错误的是( )
A.-3a<-3b B.bc>ab C.a-3>b-3 D.-2a>2bc
思路分析:(方法一)由a>0,b<0可知a>b,所以-3a<-3b,a-3>b-3,根据不等式的性质3、性质1可知是正确的;同样由a>0,c<0可知c<a,两边同乘以b,又b<0,所以bc>ab,故A、B、C皆是正确的.因此错误的选项是D.(事实上,由a>0得-2a<0;由b<0,c<0得2bc>0,所以一定有-2a<2bc,故D是错误的.)
(方法二)由于满足条件a、b、c的值,只有一个选项是错误的.从而可用特殊值法进行解答.为此,不妨设a=1,b=-1,c=-2,此时-3a=-3,-3b=3,所以-3a<-3b,A正确;bc=2,ab=-1,所以bc>ab,B正确;a-3=-2,b-3=-4,所以a-3>b-3,所以C正确,因此,错误的选项是B.
答案:D
方法点拨:做这类题时应注意:不等式的基本性质是有条件的,如果不符合其中的条件,那么运用此性质得出的结论是不对的.不等式的基本性质是解不等式的主要依据,必须熟练地掌握.要认真弄清不等式的基本性质与等式的基本性质的异同,特别是在不等式两边同乘以(或除以)同一个数时,不仅要考虑这个数不等于0,而且必须先确定这个数是正数还是负数,如果是负数,不等号的方向必须改变.
[基础能力训练]
2.设a<b,则下列各式应填“>”号的是( )
A.a-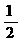 ______b-
______b-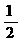 B.2a______2b
B.2a______2b
C.-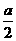 _______
_______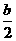 D.
D.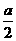 _______
_______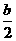
1.举例说明不等式的这3条基本性质.
3.依据不等式的性质,把下列不等式化成x>a或x<a的形式:
(1)x+3<5 (2)x-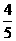 >
>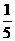 (3)
(3)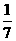 x<-3 (4)-2x<5
x<-3 (4)-2x<5
[点击思维]
2.按下列条件,写出仍能成立的不等式.
(1)-5<-2,两边都加上(-3)得:_________;
(2)0<5,两边都乘以(-3)得:_________;
(3)9<12,两边都除以(-3)得:________;
(4)a>b,两边都乘以(-8)得:________.
1.填空:
(1)不等式两边都加上(或减去)_______,不等号的方向不变.
(2)不等式两边都乘以(或除以)_______,不等号的方向不变.
(3)不等式两边都乘以(或除以)_______,不等号的方向改变.
(4)若a<b,则a+c______b+c,a-c______b-c.
(5)若a<b,则c>0,则ac______bc,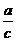 ______
______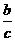 .
.
(6)若a<b,且c<0,则ac______bc,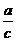 ______
______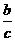 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com