
题目列表(包括答案和解析)
13.把黄豆发成豆芽后,重量可以增加7.5倍,要得到3 400千克这样的豆芽,需要多少千克黄豆?
思路解析:本题的关键词是“增加”,意思是在原有x千克的基础上,又多出7.5倍,也就变为原重量的(1+7.5)倍了.
解:设需要x千克黄豆,则(1+7.5)x=3 400,
解得x=400.
答:需要400千克的黄豆.
12.某市居民生活用电基本价格为每度0.40元,若每月用电量超过a度,超出部分按基本电价的70%收费.
(1)某户五月份用电84度,共交电费30.72元,求a.
(2)若该户六月份的电费平均为每度0.36元,求六月份共用电多少度?应交电费多少元?
思路解析:基本数量关系是:电费=用电量×每度电价.本题要注意:超出a度部分的用电量,其电价与a度以及a度以内的用电量的电价不同.
解:(1)由题意,有这样的相等关系:
a度电的电费+超出a度的那部分电费=五月份总电费,
由此得方程0.40a+(84-a)×0.40×70%=30.72,
解得a=60.
(2)设该户六月份共用电x度,由题意,有相等关系:
60度电的电费+超出60度的那部分电费=六月份总电费,
由此得方程0.40×60+(x-60)×0.40×70%=0.36x,
解得x=90,则0.36x=32.40.
答:该户六月份共用电90度,应交电费32.40元.
11.今年儿子13岁,父亲40岁,多少年后父亲的年龄是儿子年龄的2.5倍?
解:设x年后父亲的年龄是儿子年龄的2.5倍,
根据题意得40+x=2.5(x+13),解这个方程,得x=5.
答:5年后父亲的年龄是儿子年龄的2.5倍.
10.一群小孩分一堆梨,1人1个多1个,1人两个少2个,问有几个小孩、几个梨?
解:设有x个小孩,根据题意,得x+1=2x-2,
解这个方程得x=3.
当x=3时,x+1=3+1=4.
答:有3个小孩,4个梨.
9.已知关于x的方程ax+2=2(a-x),它的解满足|x+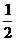 |=0,则a=____.思路解析:第一个方程中有两个字母a和x,因为由|x+
|=0,则a=____.思路解析:第一个方程中有两个字母a和x,因为由|x+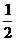 |=0可以求出x,而第一个方程中的x若与|x+
|=0可以求出x,而第一个方程中的x若与|x+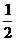 |=0的解相同,也能满足等式关系.因此将x的值代入即可求出a.
|=0的解相同,也能满足等式关系.因此将x的值代入即可求出a.
解:由|x+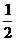 |=0,可得x=-
|=0,可得x=-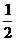 .
.
将x=-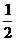 代入ax+2=2(a-x)可得
代入ax+2=2(a-x)可得
-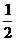 a+2=2[a-(-
a+2=2[a-(-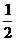 )],
)],
-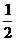 a+2=2a+1,
a+2=2a+1,
-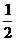 a-2a=1-2,
a-2a=1-2,
-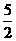 a=-1,
a=-1,
a=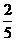 .
.
答案:
综合·应用·创新
8.解方程:5x-|x|=8.
思路解析:这是个含有绝对值的方程,我们利用绝对值的定义,分x≥0、x<0两种情况去掉绝对值符号,把它转化为一元一次方程来解.
解:(1)当x≥0时,|x|=x,
∴原方程即是5x-x=8,
4x=8,∴x=2,(符合x≥0的条件).
(2)当x<0时,|x|=-x,
∴原方程即是5x+x=8,
6x=8,∴x=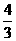 .
.
但x=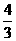 不满足x<0的条件,所以不符合要求,应舍去.
不满足x<0的条件,所以不符合要求,应舍去.
7.如果x=-2是方程3x+5=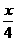 -m的解,那么m2=____.
-m的解,那么m2=____.
思路解析:x=-2是原方程的解,所以代入后会使方程左右相等.此时再将方程中的m作为未知数求解,并解出m2即可.
解:因为x=-2是3x+5=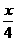 -m的解,
-m的解,
∴将x=-2代入,得
3×(-2)+5=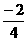 -m,
-m,
整理,得-6+5=-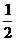 -m,
-m,
移项,得m=-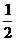 +6-5,
+6-5,
即m=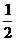 .
.
所以m2=(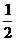 )2=
)2=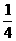 .
.
答案: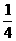
6.某面粉仓库存放的面粉运出15%后,还剩余42 500千克,这个仓库原来有多少面粉?
思路解析:通过审题找出关键词“剩余”,得出本题的文字形式的等量关系“原有的-运出的=剩余的”理解.
解:设原来有x千克面粉,那么运出了15%x千克,由题意,得
x-15%x=42 500,
解方程x-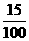 x=42 500,
x=42 500,
所以x=50 000.
答:原来有50 000千克面粉.
5.如果2x5a-4-3=0是关于x的一元一次方程,那么a=____,此时方程的解是____.
思路解析:由题意得5a-4=1,解得a=1.把a=1代入原方程,
得2x-3=0,解得x= .
.
答案:1
4.若代数式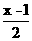 +
+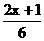 与
与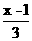 +1的值相等,则x=____.
+1的值相等,则x=____.
思路解析:由题意得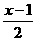 +
+ =
=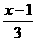 +1,解得x=2.
+1,解得x=2.
答案:2
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com