7.如图5-1-22，直线AB、CD相交于点O，OM⊥AB，若∠1=∠2，求∠NOD的度数．

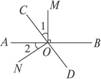
图5-1-22

解析：由条件知∠1与∠COA互余，由∠1=∠2知∠2与∠COA互余，从而可求出∠NOD．

答案：因为OM⊥AB,所以∠BOM=∠AOM=90°．

因为∠AOM=∠1+∠AOC，∠1=∠2,所以∠AOM=∠2+∠AOC=90°.

因为∠2+∠AOC=∠CON,所以∠CON=90°．

所以∠NOD=∠COD-∠CON=180°-90°=90°

综合·应用

6.如图5-1-21，直线AB、CD、EF相交于O点．∠AOF=3∠BOF，∠AOC=90°，求∠DOF的度数．

图5-1-21

解析：观察图形有：∠AOF与∠BOF互为邻补角，∠BOF与∠AOE互为对顶角，从而可求岀∠EOC的度数，而∠DOF与∠EOC为对顶角，∠DOF可求．

答案：设∠BOF=x，则∠AOF=3x,

因为x+3x=180°(邻补角定义)，

所以x=45°，即∠BOF=45°，∠AOE=45°(对顶角相等)．

又∠AOE+∠EOC=∠AOC=90°，

所以∠DOF=∠EOC=45°(对顶角相等)．

5.如图5-1-20，直线AB与CD相交于点O，若∠AOD=80°，∠BOE-∠BOC=40°,求

∠DOE的度数．

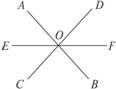
图5-1-20

解析：本题关键在于结合图形找到题中的隐含条件∠AOD与∠BOC互为对顶角，∠DOE与∠COE互为邻补角．

答案：∠BOC=∠AOD=80°，∠BOE-∠BOC=∠COE=40°，

∠DOE=180°-∠COE=140°

4.如图5-1-19，OD⊥BC，垂足为D，BD=6厘米，OD=8厘米，OB=10厘米,那么点B到OD的距离为________，点O到BC的距离为________，O、B两点间的距离为________．

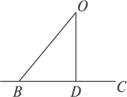
图5-1-19

解析：根据点到点的距离和点到直线的距离的定义求解．

答案：6厘米　 8厘米　 10厘米

3.如图5-1-18，OA⊥OB于O，直线CD经过O，∠AOD=35°，则∠BOC=______.

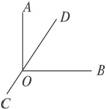
图5-1-18

解析：根据∠AOB=90°，从而求出∠BOD的度数是解本题的关键．又根据∠BOC为∠BOD的邻补角,从而容易得到答案．

答案：125°

2.如图5-1-17所示，∠AOB=∠COD=90°，则下列叙述中正确的是(　　 )

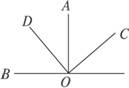
图5-1-17

A.∠AOC=∠AOD　　　　　　　　　　 B.∠AOD=∠BOD

C.∠AOC=∠BOD　　　　　　　　　　 D.以上都不对

解析：由∠AOC+∠AOD=90°，∠AOD+∠BOD=90°，从而作出判断．

答案：C

1.如图5-1-16,∠1与∠2是对顶角的是(　　 )

图5-1-16

解析：根据对顶角定义：(1)有公共端点；(2)角的两边互为反向延长线，故不难作出选择．

答案：D

9.(拓展题)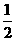 a小于a吗？2a大于a吗？a²一定大于(-a²)吗？-a³一定小于a³吗？(a-b)与(b-a)谁大谁小？

思路解析：为了要正确回答这类问题，必须搞清0与a的大小关系，这并不难，实际上，(-a)的意义是a的相反数.只要把a划分为正数，零，负数三个范围，分别比较大小，就能得出正确结论，即

答案：(1)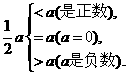

(2)

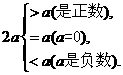
(3)

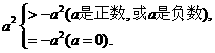
(4)

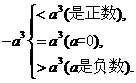
(5)

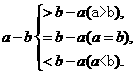
7.化简下列各数：

(1)-[-(-5)]；　　　　　　　　　 (2)-[-(+5)]；

(3)-(-m)；　　　　　　　　　　 (4)+(-a)；

(5)-(a-b)；　　　　　　　　　　 (6)-(a+b).

思路解析：(1) -[-(-5)]＝-(+5)＝-5；

(2)-[-(+5)]＝-(-5)＝+5；

(3)-(-m)＝m；

(4)+(-a)＝-a；

(5)-(a-b)＝-a+b＝b-a；

(6)-(a+b)＝-a-b.

答案：-5　 5　 m　 -a　 b-a　 -a-b

8.有理数a、b在数轴上的位置如图：

将a，-a，b，-b，1，-1用“＜”号排列出来.

思路解析：由图看出，a＞1，-1＜b＜0，|b|＜1＜|a|.-a，-b分别是a和b的相反数，数轴上表示a和-a，b和-b的点都关于原点对称，它们到原点的距离分别相等，用这个性质在数轴上画出表示-a，-b的点，它们的大小也就排列出来了.

答案：在数轴上画出表示-a、-b的点：

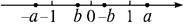
由图看出：-a＜-1＜b＜-b＜1＜a.

6.在数轴上标出2，-4.5，0各数与它们的相反数.

思路解析：先求出它们的相反数，再画数轴表示.

答案：