6.已知:如图5-9，三条直线AB、CD、EF相交于一点O，已知∠1=50°，∠5=42°，则∠2=_________，∠3=_________，∠4=_________，∠2+∠4+∠6=_________

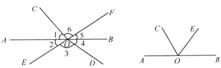
图5-9　　　　　　　　　 图5-10

答案：42°；88°；50°；180°

课下作业

5.已知∠1与∠2是对顶角，∠1与∠3是邻补角，则∠2+∠3_________.

答案：180°

4.如图5-8，直线AB、CD相交于点O，若∠AOD比∠AOC大40°，则∠BOD=_________；若∠AOD=2∠AOC，则∠BOC=_________；若∠AOD=∠AOC，则∠BOD=_________.

答案：70°；120°；90°

3.如图5-8，直线AB、CD相交于点O，射线OE为∠BOD的平分线，∠BOE=30°，则∠AOE为_________

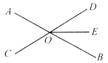
图5-8

答案：150°

2.如图5-7，直线l₁，l₂和l₃相交构成8个角，已知∠1=∠5，那么，∠5是_________的对顶角，与∠5相等的角有∠1、_________，与∠5互补的角有_________.

图5-6　　　　　　　 图5-7

答案：∠7；∠3、∠7；∠6、∠8、∠2、∠4

课上作业

课前热身

1.如图5-6，直线AB、CD相交于点O，对顶角有_________对，它们分别是_________，∠AOD的邻补角是_________.

答案：2；∠AOC与∠BOD，∠AOD与∠BCC；∠AOC，∠BOD

11.如图5-1-25，已知AOB为直线，OC平分∠BOD，EO⊥OC于O.试说明：OE平分∠AOD.请在括号中写出所依据的定理或定义.

图5-1-25

解：∵AOB是直线(已知)，

∴∠BOC+∠COD+∠DOE+∠EOA=180°(　　 ).

又∵EO⊥OC于O(已知)，

∴∠COD+∠DOE=90°(　　 )，

∴∠BOC+∠EOA=90°(　　 )，

又∵OC平分∠BOD(已知)，

∴∠BOC=∠COD(　　 )，

∴∠DOE=∠EOA(　　 )，

∴OE平分∠AOD(　　 ).

解析：因为OC平分∠BOD，所以∠BOC=∠COD.又因为EO⊥OC于O，所以

∠COD+∠DOE=90°；又因为∠BOC+∠EOA=90°，所以∠DOE=∠EOA.

答案：平角的定义　 垂直的定义　 等量减等量，差相等　 角平分线的定义　 等量减等量，差相等　 角平分线的定义

10.如图5-1-24，O是直线AB上的一点，OC⊥OD.以下两个结论:①∠AOC与∠BOD互为余角，②∠AOC、∠COD、∠BOD互为补角，它们的正确与否应是(　　 )

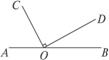
图5-1-24

A.①②都正确

B.①正确，②不正确

C.①不正确，②正确

D.①②都不正确

解析：因为OC⊥OD,所以∠COD=90°，由∠AOC+∠COD+∠BOD=180°,所以

∠AOC +∠BOD=90°，即①正确.由邻补角的定义可知邻补角指的是两角的位置关系，因此②不正确.

答案：B

9.如图5-1-23所示，∠1=70°，OE平分∠AOC．

求∠EOC和∠BOC的度数．

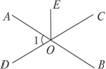
图5-1-23

解析：首先由邻补角的定义可求得∠AOC=110°，又因为OE平分∠AOC，所以∠EOC=∠AOE=55°.因为∠BOC和∠1是对顶角，由对顶角相等可知∠BOC=∠1=70°．

解：因为∠1+∠AOC=180°，又∠1=70°，

所以∠AOC=180°-70°=110°．

OE为∠AOC的平分线，所以∠E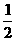OC=∠AOC=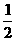×110°=55°．又因为∠BOC=∠1(对顶角相等)，

所以∠BOC=70°．

8.判断正误：

(1)过直线l外任两点P、Q，可作直线PQ⊥l.(　　 )

(2)直线外一点与直线上各点连接的所有线中，垂线段最短.(　　 )

(3)斜线段大于垂线段.(　　 )

解析：(1)P、Q确定的直线PQ不一定与直线l垂直.

(2)从直线外一点与直线上各点连接的所有线可以分为三类：线段、折线和曲线，而线段又可以分为垂线段和斜线段.由垂线段的性质可知，它是正确的.

(3)没有确定位置关系，无法比较大小.

答案：(1)错　 (2)对　 (3)错.