10、西姆松定理：点P是△ABC外接圆周上任意一点，PD⊥BC，PE⊥AC，

PF⊥AB，D、E、F为垂足，则D、E、F三点共线，此直线称为西姆松线。

9、　　 正弦定理、在△ABC中有(R为△ABC外接圆半径)

余弦定理：a、b、c为△ABC的边，则有：

　 a²=b²+c²-2bc·cosA;　　 b²=a²+c²-2ac·cosB;　　 c²=a²+b²-2ab·cosC;　　

8、　　 三角形位似心定理：如图，若△ABC与△DEF位似，则通过对应点的三直线

AD、BE、CF共点于P

7、　　 托勒密定理：四边形ABCD是圆内接四边形，则有AB·CD+AD·BC=AC·BD

6、　　 三角形内、外角平分线定理：

内角平分线定理：如图：如果∠1=∠2，则有

外角平分线定理：如图，AD是△ABC中∠A的外角平分线交BC的延长线与D，

则有

5、　　 广勾股定理的两个推论：

推论1：平行四边形对角线的平方和等于四边平方和。

推论2：设△ABC三边长分别为a、b、c，对应边上中线长分别为m_a、m_b、m_c

则：m_a=；m_b=；m_c=

4、　　 塞瓦定理的逆定理：设M、N、P分别在△ABC的

　 边AB、BC、CA上，且满足，则AN、BP、CM相交于一点。

3、　　 塞瓦定理：设O是△ABC内任意一点，AO、BO、CO分别交对边于N、P、

M，则

2、　　 梅涅劳斯定理的逆定理：如果在△ABC的三边BC、CA、AB或其延长线上

有点D、E、F，且满足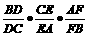=1，则D、E、F三点共线。

1、　　 梅涅劳斯定理：如果在△ABC的三边BC、CA、AB或其延长线上有点D、

E、F且D、E、F三点共线，则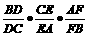=1