24、某果品公司欲请汽车运输公司或火车货运站将60吨水果从A地运到B地，已知汽车和火车从A地到B地的运输路程均为S千米，这两家运输单位在运输过程中，除都要收取的运输途中每吨每小时5元的冷藏费外，要收取的其它费用及有关运输资料用下表给出：

(1)请分别写出这两家运输单位送这批水果所收取的总费用y₁(元)和y ₂(元)(用含S的式子表示)

　　 (2)为了减少费用，你认为果品公司应选择哪家运输单位运送这批水果更为合算？(说明：“1元/吨千米”表示“每吨每千米1元”)

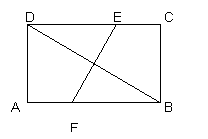
23、已知矩形ABCD中，AB= 4，BC=3，折叠矩形ABCD，使点B与点D重合，求折痕EF的长。

22、已知：抛物线y = x² + (2k + 1) x – k² + k

　　 (1)求证：此抛物线与x轴总有两个不同的交点。

　　 (2)如果该抛物线与x轴两个交点间的距离为3，求K的值。

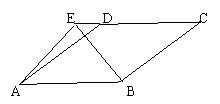
21、如图，四边形ABCD是菱形，E为CD延长线上一点，且EA = EB，

EA ⊥EB，求∠DAB的度数。

20、如图，在△ABC中，AB= AC，E是AB的中点，以点E为圆心，EB为半径画孤，交BC于点D，连结ED，并延长ED到点F，使DF = DE，连结 FC

　　 求证：∠F = ∠A

19、已知直线过点A(1，9)且平行于直线y = 3x + 4，求直线解析式。

18、设x₁，x₂是方程2x² - 3x - 8 = 0的两个根，不解方程，利用根与系数的关系，求下列各式的值。

　　 (1)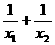　　　　　　　　　　　　 (2)(x₁ –2)( x₂ – 2)

17、解方程：3x ( x – 1 ) = 5 – 5x

16、结果四边形ABCD的两条对角线相等，它的四边的中点顺次连结得到了四边形EFGH，那么四边形EFGH是…………………………(　　 )

　　 A，菱形　　　 B，正方形　　　 C，矩形　　　 D，等腰梯形

15、下列方程中的两个实数根是x₁,x₂，满足x₁ + x₂=3的方程是(　　 )

　　 A，x² + 3x + 5 = 0　　　　　 B，x² + 3x - 5 = 0　

　　 C，x² - 3x + 5 = 0　　　　 　　D，x² - 3x - 5 = 0