
题目列表(包括答案和解析)
1、下列各式中不是二次根式的是( )
A、 B、
B、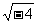 C、
C、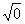 D、
D、
8.已知782+8161能被57整除,求证:783+8163也能被57整除。
7.当n为整数时,求证:n(n+1)(2n+1)为6的倍数。
6.试证: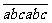 能被11整除。
能被11整除。
5.下列各数中能被11整除的数是( )
A、3312214554 B、632473 C、1234789 D、300121
4.下列各数中能被9整除的数是( )
A、60847 B、3514 C、31196 D、71235
3.下列各数中能被8整除的数是( )
A、3462 B、7432 C、5948 D、9754
2.下列各数中能被4整除的数是( )
A、534 B、724 C、962 D、3350
1.下列各数中能被3整除的数是( )
A、54327 B、64531 C、527 D、7321
2、整数的整除的常用判别方法
①被4整除的数的判别:一个数的末两位数字组成的数能被4整除,则该数必能被4整除。
②被8整除的数的判别:一个数的末三位数字组成的数能被8整除,则该数必能被8整除。
③被9整除的数的判别:一个数的各位数字之和能被3整除,则该数必能被9整除。
④被11整除的数的判别:一个数自右至左所有偶数位上的数的和与奇数位上的数的和的差能被11整除,则该数必能被11整除。
例2 判定2889304能否被11整除。
[分析]这是一个七位数,可考虑先求出其奇数位上4个数的和与其偶数位上3个数的和,利用④解之。
[解]∵4+3+8+2=17,0+9+8=17,
∴17-17=0,0能被11整除。
∴该数能被11整除,即11|2889304
练习1
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com