19.如图1所示，某筑路工程队，需要一种空心混凝土管道，它的规格是：内径d=120厘米，外径D=150厘米，长L＝200厘米.利用分解因式计算，浇筑一节这样的管道需要多少立方米的混凝土.(π取3.14，结果保留两位有效数字)

图1

解：所需混凝土为

［π()²－π(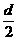)²］L=πL(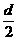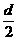－)(+)=3.14×200(75－60)(75+60)=1.2717 m³≈1.3(m³).

答：浇筑一节这样的管道需要1.3 m³的混凝土.

18.(5分)已知x+y=15，x²+y²=113，求x²－xy+y²的值.

解：∵x+y=15，∴(x+y)²=15²，x²+y²+2xy=225.

又∵x²+y²=113，∴113+2xy=225，2xy=112，xy=56.

∴x²－xy+y²=113－56=57.

17.(20分)分解因式.

(1)3(a+1)²－75(a－3)²；(2)4a^m+2b^m+1－a^mb^m－1；(3)9(a－b)²+12(a²－b²)+4(a+b)²；　　　　　　　

(4)(a+b)(a+b－2)+1－a².

答案:(1)原式=3［(a+1)²－25(a－3)²］=3［a+1－5(a－3)］［a+1+5(a－3)］=3(16－4a)(6a－14)

=24(4－a)(3a－7).

(2)原式=a^mb^m－1(4a²b²－1)=a^mb^m－1(2ab－1)(2ab+1).

(3)原式=［3(a－b)］²+12(a－b)(a+b)+［2(a+b)］²=［3(a－b)+2(a+b)］²=(5a－b)².

(4)原式=(a+b)²－2(a+b)+1－a²=(a+b－1)²－a²=(b－1)(2a+b－1).

16.小军在对a⁴+分解因式时，步骤如下：

a⁴+=a⁴+a²+－a²(添两项a²与－a²，前三项可利用完全平方公式)

＝(a²+)²－a²(写成完全平方式与最后一项又符合平方差公式)

＝(a²+a+)(a²－a+).

如果请你分解因式4x⁴+1，你第一步要完成的是

A.4x⁴+1+4x²　　　　　　　 　　　　　　　　　　 B.4x⁴+1－4x²　　　　

C.4x⁴+1+4x²－4x²　　　　　　　 　　　　　　 D.4x⁴+1+2x²－2x²

答案:C

15.若xy=1，则(x+y)²－(x－y)²等于

A.－4　　　　 　　　　 　B.4　　　　 　　　　 C.2　 　　　　　　　　　　　　　　　　 D.－2

答案:B

14.小明遇到了这样一道题：已知a、b、c是△ABC的三边长，且a²+b²+c²－6a－8b－10c+50=0，试判断△ABC的形状(按角分类)，你帮小明推一下，△ABC应属于

A.直角三角形　　　　 　B.等腰三角形　　　 C.等边三角形　　　　 　　　　　　 D.不能确定

答案:A

13.计算(－a)^m+a(－a)^m－1的值是

A.(－a)^m　　　　 　　 　B.－1　　　　 　　　　　　 C.0　　　　 　　　　　　　　　　 　　D.a^m－1?

答案:C

12.分解因式x²－y²－z²+2yz的结果是

A.(x－y－z)²　　　　　　　 　　　　　　　　　　　 B.(x+y－z)(x－y+z)

C.(x+y－z)²　　　　　　　 　　　　　　　　　　　　 D.(x－y－z)(x+y+z)

答案:B

11.两个连续奇数的平方差，一定是

A.24的倍数　　　　 　　 　B.16的倍数　　　　 C.12的倍数　　　　 　　　 　　D.8的倍数

答案:D

10.多项式(x²+y²)(x²+y²－8)+16分解因式正确的是

A.(x²+y²－4)²　　　　 B.(x－y)⁴　　　　 C.(x²－y²－4)²　　　　 D.(x²+y²+4)²

答案:A