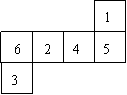
8.　　　　 下图可以沿线折叠成一个带数字的立方体，每三个带数字的面交于立方体的一个顶点，则相交于一个顶点的三个面上的数字之和最小是　 (A) 7 　　　(B) 8　　　 (C) 9　 　　　(D) 10　

7.　　　 图1是小明用八块小正方体搭的积木，该几何体的俯视图是…………(　　　 )

6.　　　 如图，CD是Rt△ABC斜边AB上的高，将△BCD沿CD折叠，B点恰好落在AB的中点E处，则∠A等于 (　　　　 )　 A．25°　 B．30°　　 C．45°　　 D．60°

5.　　　　 如图，等腰三角形ABC中，AB=AC，∠A=44°，CD⊥AB于D，则∠DCB等于A、44°　　　 B、68°　　 C、46°　　　 D、22°　　　　　　　　 (　　 )

4.　　　 以下各组数据能作为直角三角形三边长的是 (　 )A、6，11，12　　　　　　　　　　 B、5，11，12　　 C、6，12，13　 D、5，12，13

3.　　　 已知等腰三角形一边是3，一边是6，则它的周长等于(　　　 )A．12　 B．12 或15　　 C．15　　 D．18或15

2.　　　　 如图，在下列条件中，能够直接判断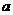∥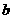的是(　　　 )A．∠1=∠4　 　 B．∠3＝∠4　 C．∠2+∠3＝180°　　　 　　　 D．∠1＝∠2

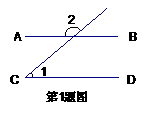
1.　　　　 如图，已知：AB∥CD，若∠1＝50°，则∠2的度数是(　　　 )A、50°　　　　 B、60°　　　　 C、130　　　　 D、120°

(三)　 互动3

一次函数和反比例函数的图象与性质：

1.一次函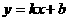(k≠0)：是一条与X轴和Y轴同时相关的直线。

K值	图象	象限		K值	图象	象限
k>0		b>0	k<0		b>0
b<0	b<0
增减性		增减性

2. 反比例函数(k≠0)的图象：双曲线

K值	图象	象限	增减性	备注
k>0		图象经过第　　 、 　　 　象限	每个象限内， y 随x的增大而　 　　　 ，随x的减小而　　　 。	两个分支部都无限地接近x轴和y轴，但永远不能到达x轴与y轴。
k<0		图象经过第　　　 、 　　　 　象限	每个象限内， y 随x的增大而　 　　　 ，随x的减小而　　　　 。

3．待定系数法：

(1)正比例函数经过(1，2)，则该解析式为　　　　　　　　 ，y随x的增大而　　　　 。

(2)反比例函数经过(－1，－3)则该解析式为　　　　　　　　 ，y随x的增大而　　　　 。

(3)一次函数经过(1，2)，(3，4)则该函数解析式为　　　　　　 　，其图象不经过第　　 象限，y随x的减小而　　　　　 。

(二)　 互动2

平面直角坐标系：

(1)坐标：在点P(x,y)中，

x叫做横坐标，y叫做纵坐标。

注：坐标平面内所有的点与所有有序实数之　　　

间是一一对应的。

(2)象限的点与符号

第一象限(？，？)；第二象限(？，？)

第三象限(？，？)；第四象限(？，？)

x轴上(±，0)；y轴上(0，±)；原点上(0，0)

注：x轴上的点，纵坐标y=0；

　　　　　 y轴上的点，横坐标x=0。

例：①一次函数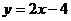与x轴的交点是　　　　　 ，与y轴的交点是　　　　　 。

②直线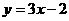经过点(　 　 ，0)、(0，　　 )。

(3)距离问题

点P(x₁，y₁)到x轴的距离 =∣y∣,到y轴的距离 =∣x∣,到原点的距离PO

例：点P(3，－4)到原点的距离是　　　　 　　。

(4)对称问题

关于X轴对称：P(a，b)　 A(a，－b)　[纵坐标改变]

关于Y轴对称：P(a，b)　　 B(－a，b)　 [横坐标改变]

关于原点对称：P(a，b)　　 C(－a，－b)　[纵、横坐标都改变]

例：点P(4，－3)与x轴对称的点的坐标是　　　，与y轴对称的点的坐标是　　　，与坐标原点对称的点的坐标是　　　。

练习：填空

(1)P(2，3)到x轴的距离是＝　　　，到y轴的距离＝　　　，到坐标原点的距离＝　　　；

(2)P(5，－2)与x轴对称的点是　　　，与y轴对称的点是　　　，与坐标原点对称的点是　　　。

(3)P在第二象限内，且横坐标与纵坐标的和是2，则点P的坐标可以是　　　。

选择题

1．下列各点中，在第三象限的点是(　　)

A、(－5，－2)　B、(－5，2)　C、(5，－2)　D、(5，2)

2．若0<a<1,则M(a-1,a)在第(　　)。

A、第一象限　 B、第二象限　 C、第三象限　 　D、第四象限

3．自变量为x≥3的函数是(　　)

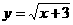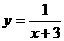A、　 B、　 C、 　D、

4．A的坐标是(5，－3)，B与A关于x轴对称，C与B关于y轴对称，D与C关于原点对称，则D的坐标为(　　)

A、(－5，－3)　 B、(－5，3)　 C、(5，－3) 　D、(5，3)