2．用求根法分解因式：

　(1)x³+x²-10x-6；

　(2)x⁴+3x³-3x²-12x-4；

　(3)4x⁴+4x³-9x²-x+2．

1．用双十字相乘法分解因式：

　(1)x²-8xy+15y²+2x-4y-3；

　(2)x²-xy+2x+y-3；

　(3)3x²-11xy+6y²-xz-4yz-2z²．

3．待定系数法

　待定系数法是数学中的一种重要的解题方法，应用很广泛，这里介绍它在因式分解中的应用．

　在因式分解时，一些多项式经过分析，可以断定它能分解成某几个因式，但这几个因式中的某些系数尚未确定，这时可以用一些字母来表示待定的系数．由于该多项式等于这几个因式的乘积，根据多项式恒等的性质，两边对应项系数应该相等，或取多项式中原有字母的几个特殊值，列出关于待定系数的方程(或方程组)，解出待定字母系数的值，这种因式分解的方法叫作待定系数法．

　例4 分解因式：x²+3xy+2y²+4x+5y+3．

　分析 由于

　(x²+3xy+2y²)=(x+2y)(x+y)，

　若原式可以分解因式，那么它的两个一次项一定是x+2y+m和x+y+n的形式，应用待定系数法即可求出m和n，使问题得到解决．

　解 设

　x²+3xy+2y²+4x+5y+3

　=(x+2y+m)(x+y+n)

　=x²+3xy+2y²+(m+n)x+(m+2n)y+mn，

　比较两边对应项的系数，则有

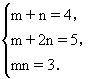
　解之得m=3，n=1．所以

原式=(x+2y+3)(x+y+1)．

　说明 本题也可用双十字相乘法，请同学们自己解一下．

　例5 分解因式：x⁴-2x³-27x²-44x+7．

　分析 本题所给的是一元整系数多项式，根据前面讲过的求根法，若原式有有理根，则只可能是±1，±7(7的约数)，经检验，它们都不是原式的根，所以，在有理数集内，原式没有一次因式．如果原式能分解，只能分解为(x²+ax+b)(x²+cx+d)的形式．

　解 设

　原式=(x²+ax+b)(x²+cx+d)

　　=x⁴+(a+c)x³+(b+d+ac)x²+(ad+bc)x+bd，

　所以有

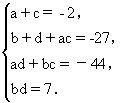
　由bd=7，先考虑b=1，d=7有

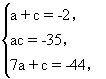
　所以

　原式=(x²-7x+1)(x²+5x+7)．

　说明 由于因式分解的唯一性，所以对b=-1，d=-7等可以不加以考虑．本题如果b=1，d=7代入方程组后，无法确定a，c的值，就必须将bd=7的其他解代入方程组，直到求出待定系数为止．

　本题没有一次因式，因而无法运用求根法分解因式．但利用待定系数法，使我们找到了二次因式．由此可见，待定系数法在因式分解中也有用武之地．

练习二

2．求根法

　我们把形如a_nxⁿ+a_n-1x^n-1+…+a₁x+a₀(n为非负整数)的代数式称为关于x的一元多项式，并用f(x)，g(x)，…等记号表示，如

　f(x)=x²-3x+2，g(x)=x⁵+x²+6，…，

　当x=a时，多项式f(x)的值用f(a)表示．如对上面的多项式f(x)

　f(1)=1²-3×1+2=0；

　f(-2)=(-2)²-3×(-2)+2=12．

　若f(a)=0，则称a为多项式f(x)的一个根．

　定理1(因式定理) 若a是一元多项式f(x)的根，即f(a)=0成立，则多项式f(x)有一个因式x-a．

　根据因式定理，找出一元多项式f(x)的一次因式的关键是求多项式f(x)的根．对于任意多项式f(x)，要求出它的根是没有一般方法的，然而当多项式f(x)的系数都是整数时，即整系数多项式时，经常用下面的定理来判定它是否有有理根．

　定理2

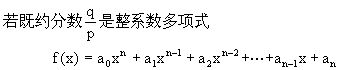
　的根，则必有p是a₀的约数，q是a_n的约数．特别地，当a₀=1时，整系数多项式f(x)的整数根均为a_n的约数．

　我们根据上述定理，用求多项式的根来确定多项式的一次因式，从而对多项式进行因式分解．

　例2 分解因式：x³-4x²+6x-4．

　分析 这是一个整系数一元多项式，原式若有整数根，必是-4的约数，逐个检验-4的约数：±1，±2，±4，只有

　f(2)=2³-4×2²+6×2-4=0，

　即x=2是原式的一个根，所以根据定理1，原式必有因式x-2．

　解法1 用分组分解法，使每组都有因式(x-2)．

　原式=(x³-2x²)-(2x²-4x)+(2x-4)

　　=x²(x-2)-2x(x-2)+2(x-2)

　　=(x-2)(x²-2x+2)．

　解法2 用多项式除法，将原式除以(x-2)，

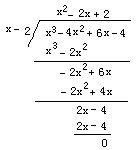
　所以

原式=(x-2)(x²-2x+2)．

　说明 在上述解法中，特别要注意的是多项式的有理根一定是-4的约数，反之不成立，即-4的约数不一定是多项式的根．因此，必须对-4的约数逐个代入多项式进行验证．

　例3 分解因式：9x⁴-3x³+7x²-3x-2．

　分析 因为9的约数有±1，±3，±9；-2的约数有±1，±

为：

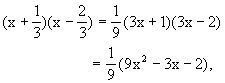
　所以，原式有因式9x²-3x-2．

　解 9x⁴-3x³+7x²-3x-2

　　=9x⁴-3x³-2x²+9x²-3x-2

　　=x²(9x³-3x-2)+9x²-3x-2

　　=(9x²-3x-2)(x²+1)

　　=(3x+1)(3x-2)(x²+1)

　说明 若整系数多项式有分数根，可将所得出的含有分数的因式化为整系数因式，如上题中的因式

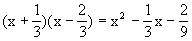
　可以化为9x²-3x-2，这样可以简化分解过程．

　总之，对一元高次多项式f(x)，如果能找到一个一次因式(x-a)，那么f(x)就可以分解为(x-a)g(x)，而g(x)是比f(x)低一次的一元多项式，这样，我们就可以继续对g(x)进行分解了．

1．双十字相乘法

　分解二次三项式时，我们常用十字相乘法．对于某些二元二次六项式(ax²+bxy+cy²+dx+ey+f)，我们也可以用十字相乘法分解因式．

　例如，分解因式2x²-7xy-22y²-5x+35y-3．我们将上式按x降幂排列，并把y当作常数，于是上式可变形为

2x²-(5+7y)x-(22y²-35y+3)，

　可以看作是关于x的二次三项式．

　对于常数项而言，它是关于y的二次三项式，也可以用十字相乘法，分解为

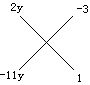
　即

　-22y²+35y-3=(2y-3)(-11y+1)．

　 再利用十字相乘法对关于x的二次三项式分解

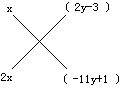
　所以

　原式=［x+(2y-3)］［2x+(-11y+1)］

　　=(x+2y-3)(2x-11y+1)．

　上述因式分解的过程，实施了两次十字相乘法．如果把这两个步骤中的十字相乘图合并在一起，可得到下图：

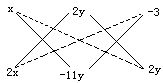
　它表示的是下面三个关系式：

　(x+2y)(2x-11y)=2x²-7xy-22y²；

　(x-3)(2x+1)=2x²-5x-3；

　(2y-3)(-11y+1)=-22y²+35y-3．

　这就是所谓的双十字相乘法．

　用双十字相乘法对多项式ax²+bxy+cy²+dx+ey+f进行因式分解的步骤是：

　(1)用十字相乘法分解ax²+bxy+cy²，得到一个十字相乘图(有两列)；

　(2)把常数项f分解成两个因式填在第三列上，要求第二、第三列构成的十字交叉之积的和等于原式中的ey，第一、第三列构成的十字交叉之积的和等于原式中的dx．

　例1 分解因式：

　(1)x²-3xy-10y²+x+9y-2；

　(2)x²-y²+5x+3y+4；

　(3)xy+y²+x-y-2；

　(4)6x²-7xy-3y²-xz+7yz-2z²．

　解 (1)

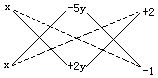
　原式=(x-5y+2)(x+2y-1)．

　(2)

　原式=(x+y+1)(x-y+4)．

　(3)原式中缺x²项，可把这一项的系数看成0来分解．

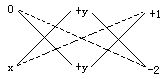
　原式=(y+1)(x+y-2)．

　(4)

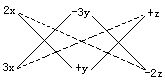
　原式=(2x-3y+z)(3x+y-2z)．

　说明 (4)中有三个字母，解法仍与前面的类似．

5．设α，β为有理数，γ为无理数，若α+βγ=0，求证：

α=β=0．

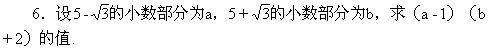
1．下列各数中哪些是有理数，哪些是无理数？为什么？

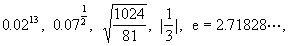
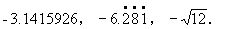
5．如图2-42所示．在正方形ABCD中，CE垂直于∠CAB的平分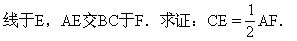

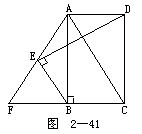
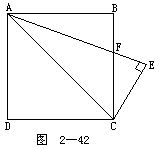
4．如图2-41所示．矩形ABCD中，F在CB延长线上，AE=EF，CF=CA．求证：BE⊥DE．

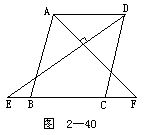
3．如图2-40所示．ABCD中，AF平分∠BAD交BC于F，DE⊥AF交CB于E．求证：BE=CF．