22、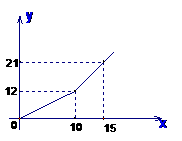(本题9分)某市为节约用水。制定了分段收费的政策，下图是一个月水费y (元)和用水量x(吨)的函数关系的图象。

(1)请写出这个函数关系的解析式及自变量x的取值范围。

(2)小明家与小敏家长期共用一只水表，五月份共用水30吨，应该付水费多少元？

(3)从六月份开始，两家各用一只水表，在两家总用水量不变(共用水30吨，两家用水量都超过了10吨)的情况下，六月份共付的水费比五月份多些还是少些？请说明理由。

21、(本题8分)某车间现有20名工人，生产甲乙两种工艺品，每名工人每天可生产6个甲种工艺品或8个乙种工艺品，一个甲种工艺品可获利10元，一个乙种工艺品可获利5元。厂方规定乙种工艺品的数量不得少于甲种工艺品的三分之一。

(1)若安排x 人生产甲种工艺品，其余工人生产乙种工艺品，车间每天的利润为y元，请写出y与x之间的函数关系式，并求自变量的取值范围。

(2)如何安排可使车间每天的利润最高，最高利润是多少？

20、(本题7分)如图，在直角坐标系中，直线y=kx+4与x 轴正半轴交于一点A，与y轴交于点B，已知△OAB的面积为10，求这条直线的解析式。

19、(本题6分)在解方程组时，想必你曾碰到过方程组无解的情况，如 。学过“一次函数与方程组”后，你能用一次函数的图象来解释这种情况吗？请用上面的例子画图说明。

18、(本题6分)已知一次函数的图象经过点(- 4，9)和(6，3)。

(1)求这个一次函数的关系式。

(2)试判断点(1，6)是否在这个函数的图象上。

17、(本题8分)在坐标系中画出函数y=-3x+4的图象，利用图象分析

(1)函数的图象经过第　　　　　　　　　　　 象限，

　 　y随x的增大而　　　　　　　　　　 。

(2)图象与x轴交于点　　　　　　　　　　　　　 ，

　　 与y轴交于点　　　　　　　　　　 。

(3)函数图象与两坐标轴围成的三角形面积为　　　　　　　　　　　　 。

(4)当　　　　　　　　　　　　 　时，y＞0； 当　　　　　　　 时，-2＜y＜1

16、已知一次函数y=(m+2)x+(3-2m)的图象不经过第四象限，则m的范围是　　　　　　　　　 。

15、直线y=3x-2经过第　　　　　　　　　　　　 象限，y随x的增大而　　　　　　　　　 。

14、将直线y=-2x+1沿y轴方向向上平移3个单位长，得到的直线解析式为　　　　　　　　　　 。

13、直线y=kx+b上有两点A(x₁，y₁)和点B(x₂，y₂)，且x₁＞x₂，y₁＜y₂，则常数k的取值范围是　　　　　　　　　　　　　　 。