4．　 一次函数y= -2x+4的图象与x轴交点坐标是　 　　　，与y轴交点坐标是　　　　 　

　图象与坐标轴所围成的三角形面积是 　　　　　.

3．　 已知一次函数y=kx+5的图象经过点(-1，2)，则k= 　　　　　.

2．　 若函数y= -2x^m+2是正比例函数，则m的值是　　　　　 .

1．　 已知一个正比例函数的图象经过点(-2，4)，则这个正比例函数的表达式是　　　 .　

　 (24)某校长暑假将带领该校市级“三好学生”去北京旅游，甲旅行社说：“如果校长买全票一张，则其余的学生可享受半价优惠.”乙旅行社说：“包括校长在内全部按票价的六折优惠.”若全票价为240元，两家旅行社的服务质量相同，根据“三好学生”的人数你认为选择哪一家旅行社才比较合算？

　 (25)某自行车保管站在某个星期日接受保管的自行车共有3500辆次，其中变速车保管费是每辆0.5元，一般车的保管费是每辆0.3元.

(1)一般车停放的辆次数为x，总的保管费为y元，试写出y与x的关系式；

(2)若估计前来停放的3500辆自行车中，变速车的辆次不小于25﹪，但不大于40﹪，试求该保管站这个星期日收入保管费总数的范围.

(26)在举国上下众志成城，共同抗击非典的非常时期，某厂接受了生产一批高质量医用口罩的任务。要求在8天之内(含8天)生产A型和B型两种型号的口罩共5万只，其中A型口罩不得少于1.8万只，该厂的生产能力是：若生产A型口罩每天能生产0.6万只，若生产B型口罩每天能生产0.8万只，已知生产一只A型口罩可获利0.5元，生产一只B型口罩可获利0.3元。设该厂在这次任务中生产了A型口罩x万只。

问：(1)该厂生产A型口罩可获利润_____万元，生产B型口罩可获利润_ ___万元；

　 　(2)设该厂这次生产口罩的总利润是y万元，试写出y关于x的函数关系式，并求出自变量x的取值范围

(3)如果你是该厂厂长：①在完成任务的前提下,你如何安排生产A型和B型口罩的只数,使获得的总利润最大?最大利润是多少?②若要在最短时间内完成任务,你又如何来安排生产A型和B型口罩的只数?最短时间是多少?

　 (21)解下列不等式(组)：(每题8分，共计24分)

(1) 5(x+2)≥1―2(x―1)　 　　　　　　(2)　

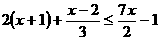
　　 (3)解不等式组：

(22)若方程组的解x、y都是正数，求a的取值范围. (6分)

(23)如图表示一艘轮船和一艘快艇沿相同路线从甲港出发到乙港行驶过程中路程随时间变化的图像．根据图像解答下列问题：(6分)

(1)在轮船快艇中，哪一个的速度较大？

(2)当时间x在什么范围内时，快艇在轮船的后面？当时间x在什么范围内时，快艇在轮船的前面？

(3)问快艇出发多长时间赶上轮船？

⑾已知“①x+y=1；②x＞y；③x+2y；④x²-y≥1；⑤x＜0”属于不等式的有　　 个.

A.2；　　　　　　　 B. 3；　　　　　　　 C.4；　　　　　　　 D. 5.

⑿如果m<n<0，那么下列结论错误的是　　　　

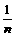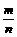A.m－9<n－9；　　　 B.-m>-n；　　　　　 C.>；　　　　　 D. >1.

(13)设“●”、“▲”、“■”表示三种不同的物体，现用天平称了两次，情况如图所示，那么●、▲、■这三种物体按质量从大到小的顺序排列为　　　

　A.■、●、▲。　　B.■、▲、●。

　 C.▲、●、■。　 D.▲、■、●。

⒁已知a，b两数在数轴上的位置如图所示，设M=a+b,N=-a+b,H=a-b，则下列各式正确的是　　　　　　

A.M>N>H；　　　　 B.H>M>N ；

C.H>M>N；　　　　 D.M>H>N.

⒂不等式组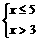的解集在数轴上表示，正确的是　　　　　　　　 ．

A.　　　　　　　　 B.　　　　　　　 　　C.　　　　　　　　　 D

⒃已知(x+3)²+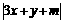＝0中，y为负数，则m的取值范围是　　　　　

A.m〉9　　　　　　　 B.m〈9　　　　　　 C.m〉－9　　　　　 D.m〈－9

⒄观察下列图像，可以得出不等式组

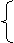　 3x+1〉0

的解集是　　　　

　　 －0.5x+1〉0

A.x〈　　　　 B.－〈x〈0

C.0〈x〈2　　　 D.－〈x〈2

⒅某种出租车的收费标准是：起步价7元(即行驶的距离不超过3千米都需付7元车费),超过3千米，每增加1千米，加收2.4元(不足1千米按1千米计算)某人乘这种出租车从甲地到乙地共付车费19元，那么此人从甲地到乙地经过的路程的最大值是

　　　　 千米.

A.11　　　　　　　　 B.8　　　　　　　　　 C.7　　　　　　　　 D.5

⒆某种肥皂原零售价每块2元，凡购买2块以上(包括2块),商场推出两种优惠销售办法.第一种：一块肥皂按原价，其余按原价的七折销售；第二种：全部按原价的八折销售.你在购买相同数量肥皂的情况下，要使第一种方法比第二种方法得到的优惠多，最少需要买　　　　　　 块肥皂.

A.5　　　　　　　　 B.4　　　　　　　　　 C.3　　　　　　　　 D.2

⒇韩日“世界杯” 期间，重庆球迷一行若干人从旅馆乘车到球场为中国队加油，现有某个车队，若全部安排乘该车队的车，每辆坐4人则多16人无车坐，若每辆坐6人，则坐最后一辆车的人数不足一半.这个车队有　　　 辆车

A.11　　　　　　　　 B.10　　　　　　　　　 C.9　　　　　　　　 D.12

　 ⑴用恰当的不等号表示下列关系：

①x的3倍与8的和比y的2倍小：　　　　　 ；

②老师的年龄a不小于你的年龄b：　　　　　　　　 .

⑵不等式3(x+1)≥5x-3的正整数解是　　　　　　　　

⑶当a　　　　　　 时，不等式(a-1)x＞1的解集是x＜.

⑷已知x＝3是方程-2＝x-1的解，那么不等式(2-)x＜的解集是　　　

⑸已知函数y=2x-3，当x　　　　 时，y≥0；当x　　　　　 时，y＜5.

　　　　　　　 X+8＜4x－1

⑹若不等式组　　　　　　 的解集是x＞3，则m的取值范围是　　　　　　　

　　　　　　　 x＞m

　　　　　　　　　　　　 x－a≥0

⑺已知关于x的不等式组　　　　　　 的整数解共有5个，则a的取值范围是　　

　　　　　　　　　　　　 3－2x＞－1

　　　　　　　 2x－a＜1

⑻若不等式组　　　　　 的解集为-1＜x＜1，那么(a-1)(b-1)的值等于　　　　

　　　　　　　 x－2b＞3

⑼小明用100元钱购得笔记本和钢笔共30件，已知每本笔记本2元，每只钢笔5元.那么小明最多能买　　　　 只钢笔.

⑽2001年某省体育事业成绩显著，据统计，在有关大赛中获得奖牌数如右表所示(单位：枚)如果只获得1枚奖牌的选手有57人，那么荣获3枚奖牌的选手最多有　　　 人.

8. 某校组织学生到距离学校6千米的光明科技馆去参观，小王因事没能乘上学校包车，于是准备在学校门口改乘出租车去光明科技馆.出租车的收费标准如下：

(1)　 写出出租车行驶的里程数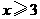(千米)与费用y(元)之间的函数关系式.

(2)　 小王身上有11元钱，求出租车到科技馆的车费够不够？请说明理由.

7. 已知一次函数y=(4m+1)x-(m+1)

(1)　 m为何值时，y随x的增大而减小？

(2)m为何值时，直线与y轴的交点在x轴的下方？

(3)m为何值时，直线位于第二、三、四象限？