4.下列关于反比例函数的意义或性质的叙述，正确的是　　 　　　　　　(　　 )

A.自变量x扩大(或缩小)几倍，函数y反而缩小(或扩大)几倍；

B.反比例函数是形如y= (k是常数，k≠0)的函数；

C.若x与y的积是一个常数，则y是x的反比例函数； D.当k＞0时，y随x的增大而增大；

3.已知一次函数y=kx–2,y随x的增大而减小，那么反比列函数y= 　(　　 )

A.当X﹥0时，y﹥0 ;　　　　 B.在每个象限内，y随x的增大而减小;

C.图象在第一，三象限 ;　　 　　D. .图象在第二，四象限;

2. 如果把分式中的x 、y同时扩大2倍，那么该分式的值 　(　　 )

A. 扩大为原来的2倍 　B. 缩小为原来的倍　 　C. 不变 　　D. 缩小为原来的倍

1. 当x为任意实数时，下列分式中一定有意义的是 　　　　　　　　　(　　 )

A. 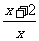　　　B. 　　　C. 　　　　D.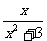

24.(本题共10分)

直角梯形OABC中BC∥OA，在如图平面直角坐标系中，已知它的各顶点坐标分别是O(0，0)，A(9，0)，B(6，4)，C(0，4)．点P从点C沿C-B-A运动，速度为每秒2个单位，点Q从A向O点运动，速度为每秒1个单位，当其中一个点到达终点时，另一个点也停止运动．两点同时出发，设运动的时间是t秒．

(1)点P和点Q 谁先到达终点？到达终点时t是多少？(请直接写出答案)

(2)当t取何值时，直线PQ∥AB ？并写出此时点P的坐标．(要写出解答过程)

(3)是否存在符合题意的t的值，使直角梯形OABC被直线PQ分成面积相等的两个部分？如果存在，求出t的值；如果不存在，请说明理由．

(4)探究：当t取何值时，直线PQ⊥AB ?(请直接写出答案，不需写出计算过程)．

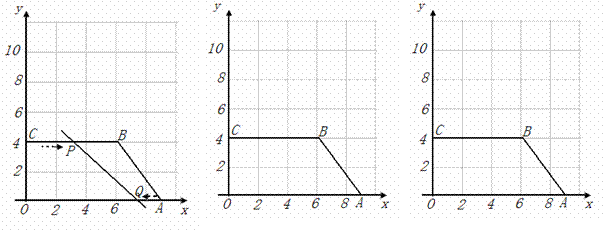图　1　　　　　　　　 图　2(备用)　　　　　　　 图　3(备用)

23. (本题共9分)

一般地，提高商品的单价，可以使每件商品获得更大的利润，但单价太高会反过来影响该商品的销售数量，只有通过合理的定价，才能取得较好的回报．小商品批发商李欣对其中一种小商品的单价与该种商品的日平均获利经过统计，得到下列数据：

(1) 根据统计所得数据，在所给的平面直角坐标系中描出相应的各点。

(2) 用线段将题(1)所画的点从左到右顺次连接，若用此图象来模拟日平均获利y关于商品的销售单价x的函数关系，分别写出函数在 1．7≤x≤1．9和1．9≤x≤2．4 时的解析式；

(3)利用题(2)所得函数关系，当日平均获利不低于83元时，求该商品的销售单价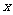 应该控制的范围．

22.(本题共6分)

如图，小明沿着河岸边的人行道散步，想顺便测一测河的宽度，在A点，他发现对岸的一棵大树C与河岸的夹角∠CAB＝45^o，继续往前走了2分钟到达点B，又测得∠ABC＝60^o，已知他步行的平均速度是1米／秒．请你帮他算一算河的宽度(精确到0．1米)．

21.(本题共6分)

如图，ABCD是平行四边形，点E在边BC延长线上，连AE交CD于点F，如果∠EAC＝∠D．

试证明：AC·BE＝AE·AB．

20. (本题共6分)

甲、乙两名射击运动员各进行10发子弹的射击，命中靶的环数如下表：

(1)在图中分别描出表示甲、乙命中靶的环数的折线图．(甲用虚线连)

(2)求得：

甲命中靶的平均环数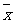_甲＝　　，

方差S²_甲＝　　；

乙命中靶的平均环数_乙＝　　　 ，

方差S²_乙= 　　　　　．

(3)如果从甲、乙两名运动员中选一名参加比赛，你认为应选谁？请说明理由．

19. 计算：(共2小题，每小题5分，共10分)

　(1)　　 　　　 (2) 　+ 6×tan30°　 +