
题目列表(包括答案和解析)
4.(每小题6分,共18分)解方程:
(1)
(2)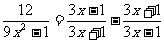
(3) (未知数为
(未知数为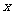 )
)
3.(每小题7分,共14分)先化简,后求值:
(1) ,其中
,其中
(2)已知: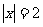 ,
,
求: 的值
的值
2.(每小题6分,共24分)计算:
(1)
(2)
(3)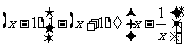
(4)
1.(每小题3分,共24分)选择题:
(1)使分式 有意义的
有意义的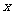 的取值范围是( )
的取值范围是( )
(A) 或
或 (B)
(B)
(C) 且
且 (D)
(D) (E)
(E)
(2)根据分式的基本性质,分式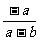 可变形为( )
可变形为( )
(A) (B)
(B)
(C) (D)
(D)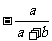
(3)化简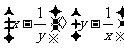 的结果为( )
的结果为( )
(A)1 (B) (C)
(C)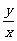 (D)
(D)
(4) 、
、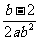 与
与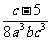 的最简公分母是(
)
的最简公分母是(
)
(A) (B)
(B)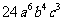
(C)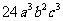 (D)
(D)
(5)把 约成最简分式为(
)
约成最简分式为(
)
(A) (B)
(B)
(C)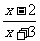 (D)
(D)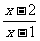
(6)使分式 的值是负数
的值是负数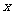 的取值范围是(
)
的取值范围是(
)
(A) (B)
(B)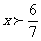
(C)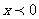 (D)不能确定的
(D)不能确定的
(7)下列各式中正确的是( )
(A) (B)
(B)
(C)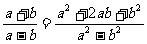 (D)
(D)
(8)可化为一元一次方程的分式方程,如果有增根,那么以下判断错误的是( )
(A) 方程只有一个增根
(B) 分式方程无解
(C) 方程还有异于增根的根
(D)增根代入最简公分母,最简公分母的值为零
已知:ΔABC中,∠A=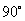 ,AD是BC边上的高,BE是角平分线,且交AD于P。
,AD是BC边上的高,BE是角平分线,且交AD于P。
(1) 求证:AE=AP;
(2)
如果∠C= ,AE=1,求AC的长。
,AE=1,求AC的长。
已知:如图,EA⊥AC于A,DC⊥AC于C,B是AC上一点,AB=CD,AE=BC。
求证:BE⊥BD。

(第六题) (第七题)
已知:如图,∠1=∠2,∠3=∠4。
求证:ED=EC。
已知:如图,线段 和
和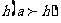
求作:等腰ΔABC,使AB=AC= ,腰上的高BD=
,腰上的高BD= 。(保留作图痕迹,不写作法)
。(保留作图痕迹,不写作法)
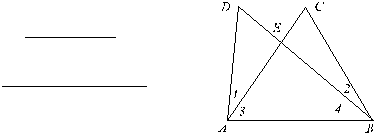
(第四题) (第五题)
(1) 三角形的高是直线 ( )
(2) 等腰三角形的腰长大于底边长 ( )
(3)
三条线段 、
、 、
、 ,如果
,如果 ,那么这三条线段一定可以组成三角形( )
,那么这三条线段一定可以组成三角形( )
(4) 等腰三角形是轴对称图形,它的对称轴是底边上的高 ( )
(5) 面积相等的两个三角形全等 ( )

(1) 等腰三角形的周长是18,一条边的长是5,则其他两边的长是______。
(2)
ΔABC中,若∠A+∠C=2∠B,最小角为 ,则最大角为______。
,则最大角为______。
(3)
已知:如图,ΔABC中,AD⊥BC于D,若AB=13,AC=8,则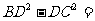 ______。
______。
(4) 已知线段AB和点C、D,且CA=CB,DA=DB。那么直线CD是线段AB的______。
(5) 一个角的平分线可以看作是______点的集合。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com