8、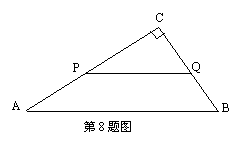如图,已知△ABC中,AB=5,BC=3,AC=4,PQ∥AB,P点在AC上(与A、C不重合)，Q在BC上.(1)当△PQC的面积与四边形PABQ的面积相等时,求CP的长.(2)当△PQC的周长与四边形PABQ的周长相等时,求CP的长.(3)试问:在AB上是否存在一点M,使得△PQM为等腰直角三角形,若不存在,请简要说明理由；若存在,请求出PQ的长.

7、如图,正方形ABCD的边长为2,AE=EB,MN=1,线段MN的两端在BC、CD上,若△AED与以M、N、C为顶点的三角形相似,求CM的长.

6、某生活小区的居民筹集资金1600元,计划在一块上、下底分别为10米,20米的梯形空地上种植花木如图①，(1)他们在△AMD和△BMC地带上种植太阳花,单价为8元/㎡，当△AMD地带种满花后(图中阴影部分)共花了160元,请计算种满△BMC地带所需费用.(2)若其余地带要种的有玫瑰和茉莉两种花木可供选择,单价分别为12元/㎡和10元/㎡，应选择哪种花木,刚好用完所筹集的资金.(3)若梯形ABCD为等腰梯形,面积不变(如图②)请你设计一种花坛图案,即在梯形内找到一点P,使得△APB≌△DPC,且S_△APD=S_△BPC，并说明你的理由.

5、将正方形ABCD折叠,使顶点A与CD边上的点M重合,折线交AD于E,交BC于F,边AB折叠后与BC交于点G,(1)如果M为CD的中点,求证:DE∶DM∶EM=3∶4∶5.(2)如果M为CD上任一点,设AB=2a，问△CMG的周长是否与点M的位置有关?若有关,请把△CMG的周长用含DM的长x(即DM=x)的代数式表示；若无关,请说明理由.

4、如图,在Rt△ABC中,∠ACB=90°，AD平分∠CAB交于点D,过点C作CE⊥AD于E,CE的延长线交AB于点F,过点E作EG∥BC交AB于G,AE·AD=16,AB=4.(1)求证:CE=EF；(2)求EG的长.

3、如图，在ABCD中,过点B作BE⊥CD,垂足为E,连结AE,F为AE上一点,且∠BFE=∠C.(1)求证:△ABF∽△EAD；(2)若AB=4,∠BAE=30°，求AE的长；(3)在(1)(2)的条件下,若AD=3,求BF的长.

2、如图,已知△ABC中，∠ACB=90°，AC=BC,点E、F在AB上,∠ECF=45°.(1)求证:△ACF∽BEC；(2)设△ABC的面积为S，求证:AF·BE=2S.

1、如图,在等腰梯形ABCD中,AD∥BC,AD=3㎝，BC=7㎝，∠B=60°，P为下底BC上一点(不与B、C重合)，连结AP,过P点作PE交DC于E,使得∠APE=∠B.(1)求证：△ABP∽△PCE；(2)求等腰梯形的腰AB的长；(3)在底边BC上是否存在一点P,使得DE∶EC=5∶3?如果存在,求出BP的长,如果不存在,请说明理由.

14、分析：

　只有利润率而无樱桃多少，价值如何，难以建立相等或不等关系，所以要设两个辅助未知数 .

解：(1)设购进大樱桃有a千克，每千克为b元，

　　 则购进大樱桃为ab元，

　　 依题意，售出应是 a(1－5%)·b(1+5%)=ab[1－(5%)²].

　　 ∵ 0<1－(5%)²<1， ∴ab[1－(5%)²]<ab.

　 这说明如果超市把每千克售价定在b(1+5%)，由于樱桃缩水，质量减少，所以超市要亏本。

　(2)设大樱桃的售价应提高x%，

13、　解：设初级机房有 x台计算机，高级机房有y台计算机，

　　依题意，得：

　　解不等式组，得

　　∵ x，y都是正整数.

　　∴ x取56、58，y取28、29，∴

　答：该校拟建的初级机房计算机若是56台，则高级机房计算机为28台；若初级机房计算机为58台，则高级机房计算机为29台。