2．某班有50人，其中三好学生10人，优秀学生干部5人，在扇形统计图上表示三好学生和优秀学生干部人数的圆心角分别是　 (　　　 ) 　A．72°，36° 　　　　　 B．100°，50°　　　　　 C．120°，60°　 D．80°，40°

1．直线y=3x+9与x轴的交点是(　 )

　　 A．(0，-3)　　　 B．(-3，0)　　 C．(0，3)　　 D．(0，-3)

27、(7分)已知等边△ABC和点P，设点P到△ABC三边的AB、AC、BC的距离分别是h₁，h₂，h₃，△ABC的高为h，请你探索以下问题：

(1)若点P在一边BC上(图1)，此时h₁、h₂、h₃与h之间有怎样的关系　　　　 ，

　 (2)若当点P在△ABC内(图2),此时h₁、h₂、h₃与h之间有怎样的关系　　　　

(3)若点P在△ABC外(图3)，此时h₁、h₂、h₃与h之间有怎样的关系　　　　 ，请写出你的猜想，并选一种情况说明理由．

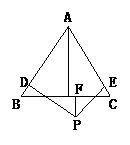
　　　　　　　 (1)　　　　　　　　　　 (2)　　　　　　　　　　　 (3)

温馨提示：考完了吗？请重新认真地检查一遍，预祝你考出好成绩！

26、(6分)某校拟派一名跳高运动员参加一项校际比赛，对甲、乙两名跳高运动员进行了8次选拔比赛，他们的成绩(单位：米)如下：

甲：1.70　 1.65　 1.68　 1.69　 1.72　 1.73　 1.68　 1.67

乙：1.60　 1.73　 1.72　 1.61　 1.62　 1.71　 1.70　 1.75

(1)　　　 要评价这2位运动员的平均水平，你选择什么统计量？求出这个统计量。

(2)　　　 请求出两组数据的方差，这两个方差的大小反映了什么？

(3)　　　 经预测，跳高1.65米就很难获得冠军，该校为了获取跳高比赛冠军，可能选哪位运动员比赛？若预测跳高1.70米方获得冠军呢？

25、(7分)如图，已知AC平分∠BAD，CE⊥AB于E，CF⊥AD于F，且BC=CD，

(1)求证：△BCE≌△DCF;　　 (3分)

(2)若AB=21，AD=9，BC=CD=10，求AC的长。　　 (4分)

24、(5分)如图所示，已知：AB=BC=AC，CD=DE=EC，求证：AD=BE．

23、如图，AD是等腰三角形ABC的底边BC上的高，DE∥AB，交AC于点E，判断△ADE是不是等腰三角形，并说明理由。(5分)

22、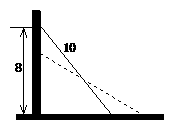(5分)如果一个长为10m的梯子，斜靠在墙上，梯子的顶端距地面的垂直距离为8m．如果梯子的顶端下滑1m，请猜测梯子底端滑动的距离是否会超过1m，并加以说明．

21、作图题：(5分)相同的小正方形搭成的几何体如图所示，请画出它的三视图。

20、如图，在一个正方形被分成三十六个面积均为1 的小正方形，点A与点B在两个格点上，问在格点上是否存在一个点C，使△ABC的面积为2，这样的点有　　　　　　 个。