3、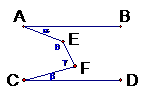如图，AB∥CD，用含α、β、γ的式子表示θ，则θ=(　　 )

(A)α+γ-β　　　　 (B)β+γ-α　　

(C)180°+γ-α-β　 (D)180°+α+β-γ

2、等腰三角形的两边分别为1和2，则其周长为(　　　　　 )

A.4　　　 B.5　　　 　　C.4或5　　　 　　D、无法确定

1、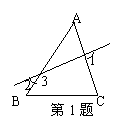如图，下列说法错误的是 (　)

A、∠C与∠1是内错角　　　　　　 B、 ∠2与∠3是内错角

C、∠A与∠B是同旁内角　　　　　 D、∠A与∠3是同位角

24、某批发商欲将一批海产品由A地运往B地，汽车货运公司和铁路货运公司均开办了海产品运输业务．已知运输路程为120千米，汽车和火车的速度分别为60千米/时和100千米/时．两货物公司的收费项目和收费标准如下表所示：

　　 注：“元/吨·千米”表示每吨货物每千米的运费；“元/吨小时”表示每吨货物每小时的冷藏费．

　　 (1)设该批发商待运的海产品有x(吨)，汽车货运公司和铁路货运公司所要收取的费用分别为y₁(元)和y₂(元)，试求出y₁和y₂和与x的函数关系式；

(2)若该批发商待运的海产品不少于30吨，为节省运费，他应该选择哪个货运公司承担运输业务？

23、如图，在平面直角坐标系中，若A点的坐标是(2，1)，B点的坐标是

(4，3)．在x轴上求一点C，使得CA+CB最短．

22、如图，△ABC是等边三角形，AE=CD，BQ⊥AD于Q，BE交AD于P．

　　 ①求∠PBQ的度数．②判断PQ与BP的数量关系．

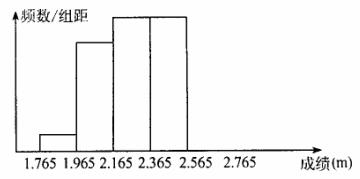
21、某校500名男生参加体育中考立定跳远测试，将所得成绩整理后分成五组，画出部分频率分布直方图，已知图中从左到右前四个小组的频率依次是0.04,0.24，0.28，0.28．

　　 (1)求第五小组的频率，并补全频率分布直方图；

　　 (2)若规定2.165m以上为满分，试问该校男生立定跳远得满分的人数有多少?

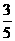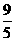20、在平面直角坐标系中有两条直线：y=x+和y=-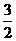x+6，它们的交点为P，且它们与x轴的交点分别为A，B．

(1)求A，B，P的坐标;(2)求△PAB的面积．

19、如图，△ABC、△ECD都是等腰直角三角形，且C在AD上．AE的延长线与BD交于P．请你在图中找出一对全等的三角形，并写出证明他们全等的过程．

18、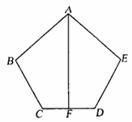已知：如图，AB＝AE，BC＝ED，AF是CD的垂直平分线，

求证：∠B＝∠E．