
题目列表(包括答案和解析)
3、用简便方法计算(写过程)
⑴ 92×88
⑵ 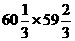 ⑶
⑶ ⑷
⑷
2、计算题(写过程)
⑴ ⑵
⑵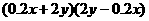 ⑶
⑶
⑷ ⑸
⑸  ⑹
⑹
1、填空题
⑴ (b + a)(b-a) = _______________, (x-2) (x + 2) = _________________;
⑵ (3a + b) (3a-b) =________________, (2x2-3) (-2x2-3) = ______________________;
⑶ 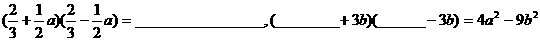
⑷ (x + y) (-x + y) = ______________, (-7m-11n) (11n-7m) = ____________________;
⑸  ;
;
10、宁启铁路泰州火车站有某公司待运的甲种货物1530吨,乙种货物1150吨,现计划用50节A、B两种型号的车厢将这批货物运至北京.已知每节A型货厢的运费是0.5万元,每节B型货厢的运费是0.8万元;甲种货物35吨和乙种货物15吨可装满一节A型货厢,甲种货物25吨和乙种货物35吨可装满一节B型货厢,按此要求安排A、B两种货厢的节数,共有几种方案?请你设计出来,并说明哪种方案的运费最少,最少运费是多少?
。
实际完成时间 家长签字
9、
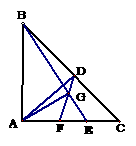 在RT△ABC中,AB=AC,∠BAC=900,D是BC的中点,G是BE上一点,E是AC上一点,∠FGE=450。
在RT△ABC中,AB=AC,∠BAC=900,D是BC的中点,G是BE上一点,E是AC上一点,∠FGE=450。
1)求证:AB2 =BG×BE
2)求证: AG ⊥BE
3)若E是AC的中点,球EF:FD的值。
8、 如图,在Rt△ABC中,已知AB=BC=CA=4cm,AD⊥BC于D,点P、Q分别从B、C两点同时出发,其中点P沿BC向终点C运动,速度为1cm/s;点Q沿CA、AB向终点B运动,速度为2cm/s,设它们运动的时间为x(s)。
如图,在Rt△ABC中,已知AB=BC=CA=4cm,AD⊥BC于D,点P、Q分别从B、C两点同时出发,其中点P沿BC向终点C运动,速度为1cm/s;点Q沿CA、AB向终点B运动,速度为2cm/s,设它们运动的时间为x(s)。
⑴ 求x为何值时,PQ⊥AC;
⑵ 设△PQD的面积为y(cm2),当0<x<2时,求y与x的函数关系式;
⑶ 当0<x<2时,求证:AD平分△PQD的面积;
7、 如图,已知P是口ABCD的边DC延长线上一点,AP分别交BD、BC于M、N。
如图,已知P是口ABCD的边DC延长线上一点,AP分别交BD、BC于M、N。
求证:(1)AM2=MN•MP
(2)
6、 如图,在△ABC中,D为AC上一点,CD=2DA,∠BAC=450,∠BDC=600,CE⊥BD于E,连接AE。
如图,在△ABC中,D为AC上一点,CD=2DA,∠BAC=450,∠BDC=600,CE⊥BD于E,连接AE。
1)写出图中所有的相等的线段并证明;
2)图中是否有相似三角形,若有,请写出一对,若没有,说明理由;
3)求△BEC与△BEA的面积比。
5、关于x的一次函数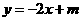 和反比例函数
和反比例函数 的图像都经过点A(
的图像都经过点A( 2,1)。
2,1)。
1)求一次函数和反比例函数的解析式;
2)求一次函数与反比例函数的另一个交点B;
3)求 的面积。
的面积。
3、解不等式:
4先化简,再求值:(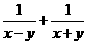 )÷
)÷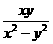 ,其中x=
,其中x=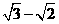 ,y=
,y= .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com