1、给定三角形的三边长，你能否判定它是不是直角三角形？

5、在直角三角形中，如果两直角边之和为17，两直角边之平方差为119，求斜边的长。

4、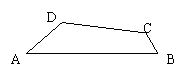如图，在四边形ABCD中，AB=8，BC=1，∠DAB=30°，∠ABC=60°，四边形ABCD的面积为5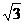，求AD的长。

3、在△ABC中，∠C=Rt∠，BC=a，AC=b，AB=c。

(1)a=9，b=12，求c；　　 (2)a=9，c=41，求b；

(3)a=11，b=13，求以c为边的正方形的面积。

2、选择题：已知有不重合的两点A和B，以点A和点B为其中两个顶点作位置不同的等腰直角三角形，一共可以作出(　　 )

A、2个　　 B、4个　　 C、6个　　 D、8个

3、学会勾股定理的简单应用。

基础训练：1、填空题：

(1)勾股定理说的是　　　　　　　　　　　　　　　　　　　　　 。

(2)直角三角形的两边长分别是3cm、4cm，则第三边长是　　　　　　　 。

(3)直角三角形的周长是24cm，斜边上的中线长为5cm，则此三角形的面积是　　 。

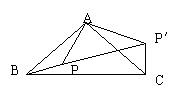
(4)如图，△ABC是Rt△，BC是斜边，P是三角形内一点，将△ABP绕点A逆时针旋转后，能与△ACP′重合，如果AP=3，那么PP′的长等于　　　　 。

2、了解勾股定理的面积证法及其数形结合思想；

2.6探索勾股定理(1)

本课重点：1、掌握勾股定理的内容；

18、如图，AD=BC，DE⊥AC，BF⊥AC，E，F是垂足，DE=BF。请你说明(1)∠DAE=∠BCF；(2)AB∥CD成立的理由。