
题目列表(包括答案和解析)
4、(1)直线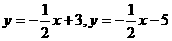 和
和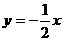 的位置关系是
,直线
的位置关系是
,直线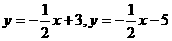 可以看作是直线
可以看作是直线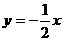 向 平移 个单位得到的;; 向 平移 个单位得到的
向 平移 个单位得到的;; 向 平移 个单位得到的
(2)将直线y=-2x+3向下平移5个单位,得到直线 .
(3).函数y=kx-4的图象平行于直线y=-2x,求函数若直线 的解析式为 ;
的解析式为 ;
(4)直线y=2x-3可以由直线y=2x经过 单位而得到;直线y=-3x+2
可以由直线y=-3x经过 而得到;直线y=x+2可以由直线y=x-3经过
而得到.
(5)直线y=2x+5与直线 ,都经过y轴上的同一点( 、 )
,都经过y轴上的同一点( 、 )
[B组]
2、3、说出直线y=3x+2与 ;y=5x-1与y=5x-4的相同之处.
;y=5x-1与y=5x-4的相同之处.
解 :直线y=3x+2与 的
,相同,所以这两条直线
,同一点,且交点坐标
,;直线y=5x-1与y=5x-4的
相同,所以这两条直线
,.
的
,相同,所以这两条直线
,同一点,且交点坐标
,;直线y=5x-1与y=5x-4的
相同,所以这两条直线
,.
1、在同一平面直角坐标系中画出下列每组函数的图象.
(2) y=2x与y=2x+3
|
x |
|
|
|
|
|
y=2x |
|
|
|
|
|
y=2x+3 |
|
|
|
|
解

3、(1)直线y=-3x和y=-3x+2、y=-3x-3的位置关系是 ,直线y=-3x-3可以看作是直线y=-3x向 平移 个单位得到的
直线y=-3x+2可以看作是直线y=-3x向 平移 个单位得到的
环节三:课堂练习----一课一练(画一次的图象与图象的平移关系)
[A组]
2、对于函数y=kx+b (k、b是常数,k≠0),常数k和b的取值对于图象的位置各有什么影响呢?
(1)当k相同,b不相同时(如y=-3x、y=-3x+2、y=-3x-3),有
共同点:______________________________________________________;
不同点:______________________________________________________.
(2)当b相同,k不相同时(如y=-3x+2与y= +2
+2
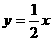 -3与y=-3x-3),有:
-3与y=-3x-3),有:
共同点:______________________________________________________;
不同点:______________________________________________________
1、通过画图,我们可以发现:
一次函数y=kx+b(k≠0)的图象是 .
特别地,正比例函数y=kx(k≠0)的图象是经过 的一条 .
根据“__点确定一条直线”,以后我们画一次函数图象时,只需确定 个点
二点法的练习:(书上的例1)
例1、在同一平面直角坐标系中画出下列每组函数的图象.
(1) y=2x与y=2x+3
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
y=2x |
|
|
|
|
|
|
|
|
|
|
|
|
y=2x+3 |
|
|
|
|
|
|
|
|
|
|
|
(2)y=2x+1与 .
.
解
|
|
|
|
|
y=2x+1 |
|
|



1、请在同一个平面直角坐标系中画出了下列函数的图象.
(1) 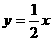 ;
;
 ;
;
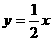 -3
-3
|
x |
… |
|
|
|
|
|
|
… |
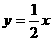 |
… |
|
|
|
|
|
|
… |
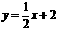 |
|
|
|
|
|
|
|
|
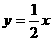 -3 -3 |
|
|
|
|
|
|
|
|
(2) y=-3x; y=-3x+2;
y=-3x-3
y=-3x; y=-3x+2;
y=-3x-3
|
x |
… |
|
|
|
|
|
… |
|
y=-3x |
… |
|
|
|
|
|
… |
|
y=-3x +1 |
|
|
|
|
|
|
|
 y=-3x +1 y=-3x +1 |
|
|
|
|
|
|
|
环节二:探讨一次函数图象的形状及其性质
[教学目标]1.通过动手画一次函数的图象,接受一次函数图象是直线的事实
2.通过画函数图象,进一步感知一次函数图象的性质
[教学重点]通过画函数图象,归纳出一次函数图象的性质
[教学过程]
环节一:画画一次函数的图象
15、已知y与 成正比例,当
成正比例,当 时,
时,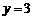 .⑴ 写出y与x之间的函数关系式;⑵ y与x之间是什么函数关系;⑶ 求x=2.5时,y的值
.⑴ 写出y与x之间的函数关系式;⑵ y与x之间是什么函数关系;⑶ 求x=2.5时,y的值
一次函数的图象的学案
14、.某油库有一没储油的储油罐,在开始的8分钟时间内,只开进油管,不开出油管,油罐的进油至24吨后,将进油管和出油管同时打开16分钟,油罐中的油从24吨增至40吨.随后又关闭进油管,只开出油管,直至将油罐内的油放完.假设在单位时间内进油管与出油管的流量分别保持不变.写出这段时间内油罐的储油量y(吨)与进出油时间x(分)的函数式及相应的x取值范围.
(在第一阶段: y=3x(0≤x≤8);
在第二阶段: y=16﹢x(8≤x≤16);
在第三阶段: y=﹣2x﹢88(24≤x≤44).)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com