4、已知直线的图象经过点(2，0)，(4，3)，(m，6)，求m的值。

．

[C组]

3、 已知y与x－3成正比例，当x＝4时，y＝3．

(1)写出y与x之间的函数关系式；

(2)y与x之间是什么函数关系；

(3)求x＝2.5时，y的值．

2、求满足下列条件的函数解析式：

(1)图象经过点(1，－2)的正比例函数的解析式；

　(2)与直线y=－2x平行且经过点(1, -1)的直线的解析式；

　(3)经过点(0，2)和(1，1)的直线的解析式；

　(4)直线y=2x－3关于x轴对称的直线的解析式；

　(5)把直线Y==2x+1向下平移两个单位，再向右平移3个单位后所得直线的解析

式．

[B组]

1、根据下列条件写出相应的函数关系式．

(1)若直线y＝m+1经过点(1,2)，则该直线的解析式是　 　　　　　　　　　　　　

(2)一次函数y=kx + b的图象如图所示，则k,b的值分别为(　 )

　 A.-，1　 B.-2，1　　 C. ，1　　 D.2，1

　(3)已知一次函数的图象经过点A(－3，－2)和点B(1,6)．

　　 ①求此一次函数的解析式，　　　　　　 　并画出图象；

　　 ②求此函数图象与坐标轴围成的三角形的面积．　　　　　　 　

(4)一次函数中，当x＝1时，y＝3；当x＝-1时，y＝7．　　　　　　

3、已知弹簧的长度 y(厘米)在一定的限度内是所挂重物质量 x(千克)的一次函数．现已测得不挂重物时弹簧的长度是6厘米，挂4千克质量的重物时，弹簧的长度是7.2厘米．求这个一次函数的关系式．

解：设所求函数的关系式是y＝　　　　　 　，根据题意，得

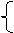
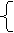　　　　 解得：　　　　 k=　　　 　

　　　　　　　　　　　　 b=　　　

∴ 所求函数的关系式是 　　　　　　　　

环节三：一课一 练

[A组]

1、根据条件，求出下列函数的关系式：

(1) 函数y=kx(k≠O，K为常数)中，当x=2时，y=－6，则k=　　　　　 　，

　　 函数关系式为y= 　　　　　

(2)直线y＝kx+5经过点(－2，－1)，则k=　　　 　，函数关系式为y= 　　　　　

(3)一次函数中，当x＝1时，y＝3；当x＝－1时，y＝7．

　 解：设所求函数的关系式是y＝kx+b，根据题意，得

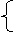
　　　　 解得：

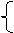　　　　　　　　 k=　　　 　

　　　　　　　　 b=　　　

　　　 ∴ 所求函数的关系式是 　　　　　　　　

2、水池已有水bm³(b为常数)，现以km³/分钟(k为常数)的速度向水池注水，则水池中水的体积y(m³)与注水时间x(分钟)之间的函数关系式为　　　　　

(1)水池已有水bm³(b为常数)，现以2m³/分钟的速度向水池注水，5分钟后水池中水的体积为25m³，则b=　　　　 　。

(2)水池已有水15m³，现打开水管，以km³/分钟的速度向水池注水，5分钟后，水池中水的体积为30 m³，则k= 　　　　　。

(3)水池已有水bm³(b为常数)，现以km³/分钟(k为常数)的速度向水池注水，3分钟后水池中水的体积为16m³，8分钟后水池中水的体积为26m³，则

　　 b=　　　　 　，k= 　　　　　。

环节二：例题练习

[教学目标]使学生通过实际问题，感受待定系数法的意义，并学会使用待定系数法求简单的函数关系式

[教学重点]使学生能应用待定系数法求一次函数的解析式，渗透常量与变量、已知和未知可以相互转化的思想方法

[教学过程]

环节一：试求一次函数解析式中的某些常量

1、水池已有水10m³，现以2m³/分钟的速度向水池注水，则水池中水的体积y(m³)与注水时间x(分钟)之间的函数关系式为　　　　　　　　　 　

12． 已知一次函数y＝(3m-8)x+1-m图象与y轴交点在x轴下方，且y随x的增大而减小，其中m为整数.

(1)求m的值；(2)当x取何值时，0＜y＜4？

函数九的学案第5课时(待定系数法)

11.已知关于x的一次函数y＝(-2m+1)x+2m2+m-3.

(1)若一次函数为正比例函数，且图象经过第一、第三象限，求m的值；

(2)若一次函数的图象经过点(1，-2),求m的值.