28、如图四边形ABCD是校园内一边长为a+b的正方形土地(其中a＞b)示意图，现准备在这块正方形土地中修建一个小正方形花坛，使其边长为a－b，其余的部分为空地，留作道路用，请画出示意图。　　　　　　

(1) 用尺规画出两种图形的情形，保留痕迹，不写作法，并标明各部分面积的代数式。

(2) 用等式表示大小正方形及空地间的面积关系。

附1：

中考热点透视

《分解因式》一章中，我们主要学习了分解因式的概念、会用两种方法分解因式，即提公因式法、平方差公式和完全平方公式(直接用公式不超过两次)进行因式分解(指数是正整数). 具体要求有：

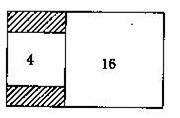
27、如图大正方形的面积为16，小正方形的面积为4，求阴影部分的面积。

26、化简求值：

　　　 (1) (x²+3x)(x－3)－x(x－2)²+(－x－y)(y－x)，其中x＝3，y＝－2；

　　　 (2) 已知x²－3x+1＝0，求下列各式的值，

　　　　　　　 ①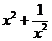；　　　　　　　 ②.

25、解方程或不等式：

　　　 (1) 3(x+2)²+(2x－1)²－7(x+3)(x－3)＝28；

　　　 (2) (1－3x)²－(2x－1)²＞5(x－1)(x+1).

24、因式分解：

　　　 (1) (a－3)²－(6－2a)；

　　　 (2) 81(a+b)²－4(a－b)²；

　　　 (3) (x²－5)²+8(5－x²)+16.

23、计算：

　　　 (1) (－2y³)²+(-4y²)³－[(－2y)²·(-3y²)²]；

　　　 (2) (3x+2)²－(3x－2)²+(3x+2)²·(3x－2)²；

　　　 (3) 3.7654²+0.4692×3.7654+0.2346².

22、已知x²+ax－12能分解成两个整系数的一次因式的积，则符合条件的整数a的个数是(　)

A、3个　　　　　　　　 B、4个　　　　　　　　 C、6个　　　　　　　　 D、8个

21、若m²+m－1＝0，则m³+2m²+3＝(　)

A、2　　　　　　　　　　 B、4　　　　　　　　　　 C、－2　　　　　　　　 D、－4

20、若二次三项式ax²+bx+c＝(a₁x+c₁)(a₂x+c₂)，则当a＞0，b＜0，c＞0时，c₁，c₂的符号为(　)

A、c₁＞0, c₂＞0　　 B、c₁＜0, c₂＜0　　 C、c₁＞0, c₂＜0　　 D、c₁, c₂异号

19、不等式(x－1)²－(x+1)(x－1)+3(x+1)＞0的正整数解为(　)

A、1, 2　　　　　　　　 B、1, 2, 3　　　　　　 C、1, 2, 3, 4　　　　 D、任意正整数