7．(探究题)当x______时，分式无意义．

题型3：分式值为零的条件的应用

6．(辨析题)下列各式中，无论x取何值，分式都有意义的是(　 )

　　 A．　　 B．　　 C．　　 D．

5．(探究题)下列分式，当x取何值时有意义．

(1)；　　　　　　　　　　　 (2)．

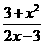4．(辨析题)下列各式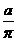，，x+y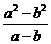，，-3x²，0中，是分式的有___________；是整式的有___________；是有理式的有_________．

题型2：分式有无意义的条件的应用

3．甲种水果每千克价格a元，乙种水果每千克价格b元，取甲种水果m千克，乙种水果n千克，混合后，平均每千克价格是_________．

课中合作练

题型1：分式、有理式概念的理解应用

2．表示_______÷______的商，那么(2a+b)÷(m+n)可以表示为________．

1．________________________统称为整式．

16.1.1　 从分数到分式

第1课时

课前自主练

16．解：假设存在三个正整数，它们的和与积相等．

　　 不妨设这三个正整数为a、b、c，且a≤b≤c，则abc=a+b+c (※)

　　 所以abc=a+b+c≤c+c+c=3c，所以ab≤3，

　　 若a≥2，则b≥a≥2，所以ab≥4，与ab≤3矛盾。

　　 因此a=l，b=l或2或3，

　　 ①　 当a=l，b=l时，代入等式(※)得l+l+c=1·1·c，c不存在；

　　 ⑦　 当a=l，b=2时，代入等式(※)得1+2+c=1·2·c，c=3；

　　 ③　 当a=1，b=3时，代入等式(※)得1+3+c=1·3·c，c=2；与b≤c矛盾，舍去

所以a=1，b=2，c=3，因此假设成立．即存在三个正整数，它们的和与积相等．

14. 180-15x≥16　 15. (1)> >　 = (2) a²+b²≥2ab　 (3) 因为(a-b)² ≥0,故 a²+b²≥2ab